【题目】定义新运算：a*b=a（b﹣1），若a、b是关于一元二次方程x2﹣x+ 
m=0的两实数根，则b*b﹣a*a的值为 ．
【答案】0
【解析】解：∵a、b是关于一元二次方程x2﹣x+ 
m=0的两实数根， ∴a2﹣a=﹣ m，b2﹣b=﹣ m，
∴b*b﹣a*a=b（b﹣1）﹣a（a﹣1）=b2﹣b﹣（a2﹣a）=﹣ m﹣（﹣ m）=0．
所以答案是：0．
【考点精析】认真审题，首先需要了解根与系数的关系(一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商)，还要掌握实数的运算(先算乘方、开方，再算乘除，最后算加减，如果有括号，先算括号里面的，若没有括号，在同一级运算中，要从左到右进行运算)的相关知识才是答题的关键．
中考解读考点精练系列答案
各地期末复习特训卷系列答案科目：初中数学 来源： 题型：
【题目】定义：对于一个有理数x，我们把[x]称作x的对称数.
若
，则[x]=x-2:若x<0，则[x]=x+2.例：[1]=1-2=-1，[-2]=-2+2=0
（1）求[
][-1]的值；
（2）已知有理数a>0.b<0，且满足[a]=[b]，试求代数式
的值：
（3）解方程：[2x]+[x+1]=1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若关于y的一元二次方程ky2﹣4y﹣3=3y+4有实根，则k的取值范围是（ ）
A.k＞﹣ 
B.k≥﹣ 且k≠0
C.k≥﹣
D.k＞ 且k≠0
查看答案和解析>>
科目：初中数学 来源： 题型：
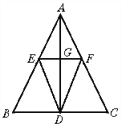
【题目】如图，在等腰三角形ABC中，AB＝AC，AD是BC边上的高，点E,F分别是边AB,AC的中点，且EF∥BC.
（1）试说明△AEF是等腰三角形；
（2）试比较DE与DF的大小关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
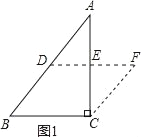
【题目】在△ABC中，沿图示的中位线DE剪一刀，拼成如图1所示的平行四边形BCFD．请仿上述方法，按要求完成下列操作设计，并在规定位置画出图示：
（1）在△ABC中，若∠C＝90°，沿着中位线剪一刀，可拼成矩形或等腰梯形，请将拼成的图形画在图2位置（只需画一个）；
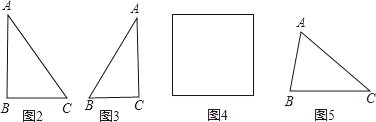
（2）在△ABC中，若AB＝2BC，沿着中位线剪一刀，可拼成菱形，并将拼成的图形画在图3位置；
（3）在△ABC中，需增加什么条件，沿着中位线剪一刀，拼成正方形，并将拼成的图形和符合条件的三角形一同画在图4位置；
（4）在△ABC中，若沿着某条线剪一刀，能拼成等腰梯形，请将拼成的图形画在图5位置（保留寻求剪裁线的痕迹）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
