
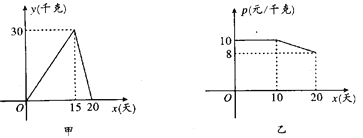
【题目】某个体户购进一批时令水果,20天销售完毕,他将本次的销售情况进行了跟踪记录,根据所记录的数据绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲,销售单价P(元/千克)与销售时间x(天)之间的关系如图乙。
(1)求y与x之间的函数关系式。
(2)分别求第10天和第15天的销售金额。
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
【答案】(1)当![]() ;(2)第10天:200元,第15天:270元;(3)最佳销售期有5天,最高为9.6元.
;(2)第10天:200元,第15天:270元;(3)最佳销售期有5天,最高为9.6元.
【解析】
(1)分两种情况进行讨论:①0≤x≤15;②15<x≤20,针对每一种情况,都可以先设出函数的解析式,再将已知点的坐标代入,利用待定系数法求解;
(2)日销售金额=日销售单价×日销售量.由于第10天和第15天在第10天和第20天之间,当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数关系式为p=mx+n,由点(10,10),(20,8)在p=mx+n的图象上,利用待定系数法求得p与x的函数解析式,继而求得10天与第15天的销售金额.
(3)日销售量不低于24千克,即y≥24.先解不等式2x≥24,得x≥12,再解不等式﹣6x+120≥24,得x≤16,则求出“最佳销售期”共有5天;然后根据![]() .(10≤x≤20),利用一次函数的性质,即可求出在此期间销售时单价的最高值.
.(10≤x≤20),利用一次函数的性质,即可求出在此期间销售时单价的最高值.
解:(1)①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,
∵直线y=k1x过点(15,30),∴15k1=30,解得k1=2.
∴y=2x(0≤x≤15);
②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b,
∵点(15,30),(20,0)在y=k2x+b的图象上,
∴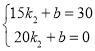 ,解得:
,解得:![]() .
.
∴y=﹣6x+120(15<x≤20).
综上所述,可知y与x之间的函数关系式为: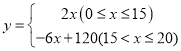 .
.
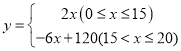 .
.
(2)∵第10天和第15天在第10天和第20天之间,
∴当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数解析式为p=mx+n,
∵点(10,10),(20,8)在z=mx+n的图象上,![]() ,
,
解得: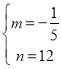 .
.
∴![]() .
.
当x=10时,![]() ,y=2×10=20,销售金额为:10×20=200(元);
,y=2×10=20,销售金额为:10×20=200(元);
当x=15时,![]() ,y=2×15=30,销售金额为:9×30=270(元).
,y=2×15=30,销售金额为:9×30=270(元).
故第10天和第15天的销售金额分别为200元,270元.
(3)若日销售量不低于24千克,则y≥24.
当0≤x≤15时,y=2x,
解不等式2x≥24,得x≥12;
当15<x≤20时,y=﹣6x+120,
解不等式﹣6x+120≥24,得x≤16.
∴12≤x≤16.
∴“最佳销售期”共有:16﹣12+1=5(天).
∵![]() (10≤x≤20)中
(10≤x≤20)中![]() <0,∴p随x的增大而减小.
<0,∴p随x的增大而减小.
∴当12≤x≤16时,x取12时,p有最大值,此时![]() =9.6(元/千克).
=9.6(元/千克).
故此次销售过程中“最佳销售期”共有5天,在此期间销售单价最高为9.6元


科目:初中数学 来源: 题型:
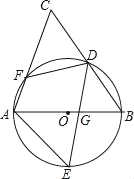
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 、
、![]() 两个点对应的数分别是
两个点对应的数分别是![]() 、
、![]() ,且满足
,且满足![]() ;
;
![]()
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是数轴上
是数轴上![]() 、
、![]() 之间的一个点,使得
之间的一个点,使得![]() ,求出点
,求出点![]() 所对应的数;
所对应的数;
(3)点![]() ,点
,点![]() 为数轴上的两个动点,点
为数轴上的两个动点,点![]() 从
从![]() 点以3个单位长度每秒的速度向右运动,点
点以3个单位长度每秒的速度向右运动,点![]() 同时从
同时从![]() 点以2个单位长度每秒的速度向左运动,设运动时间为
点以2个单位长度每秒的速度向左运动,设运动时间为![]() 秒,若
秒,若![]() ,求时间
,求时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会4×100米是最精彩的比赛项目,下表是七年级1班与2班在比赛时各运动员的接棒时间(假设每名运动员跑步速度不变,交接棒时间忽路不计,每名运动员都恰好跑100m,两个班级均用了55秒的时间达到终点(单位:秒):
班级 | 第二棒接棒时间 | 第三棒接棒时间 | 第四棒接棒时间 |
1班 | 12 | 28 | 40 |
2班 | 13 | 25 | 41 |
(1)两个班级共八名学生中跑的最慢的学生跑完100米用的时间是 秒;
(2)当2班第二棒运动员接棒时,1班运动员领先 米;
(3)求从出发开始计时,多长时间两队第一次并列?
查看答案和解析>>
科目:初中数学 来源: 题型:
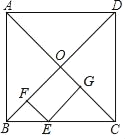
【题目】如图,在正方形ABCD中,边长为4,对角线AC、BD交于点O,点E是BC边上任意一点,分别向BD、AC作垂线,垂足分别为F、G,则四边形OFEG的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了保护和改善生态环境,决定从2014年起进行“退耕还林”,把易造成水土流失的坡耕地变为林地,并出台了一项激励措施:在“退耕还林”的过程中,每一年新增林地面积达到10亩的农户,当年都可得到生活补贴1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经“退耕还林”后的林地从下一年起,平均每亩每年可有110元的种树收入.下表是某农户在头两年通过“退耕还林”每年获得的总收入(年总收入=生活补贴费+政府奖励费+种树收入)情况:
年份 | 新增林地亩数 | 年总收入 |
2014 | 20亩 | 2400 |
2015 | 26亩 | 4300元 |
(1)试根据以上提供的资料求a的值;
(2)如果该农户计划在2016年总收入达到10000元,则该农户在2016年应新增林地约多少亩?(结果保留整数)
(3)从2015年起,如果该农户每年新增林地的亩数均能比前一年按相同的增长率增长,那么该农户在2017年新增林地多少亩(结果保留两位小数)?2017年该农户通过“退耕还林”获得的年总收入将达到多少元(结果保留一位小数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
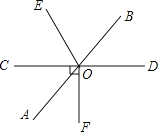
【题目】如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=65°,求∠AOF的度数;
(2)若∠BOD:∠BOE=1:2,求∠AOF的度数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com