
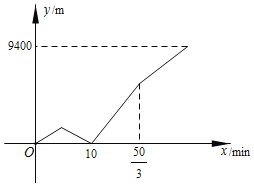
����Ŀ��ij�գ����������г���λ�ڼ���������������������ֻᣮ�������5���Ӻ����г����ֹ��϶��ҷ���û�д�Ǯ��������������绰֪ͨ�ڼҿ���ֽ�İְ������г�������Ǯ��������绰�Ͱְ������ŵ�ʱ����Բ��ƣ���ͬʱ������ԭ��һ����ٶ��������г������������������ְֽӵ��绰�����̳��������ޣ�������ͬʱ���������ϳ�����ְ��ٶȵ�2�����������������Ͱְֽ�Ǯ��������ʱ����Բ��ƣ���ͬʱ�ְ����̵�ͷ��ԭ�ٸϵ�λ�ڼ�������3900�Ĺ�˾�ϰ࣬������ޱȰְ��絽��Ŀ�صģ������������У����Ͱְֱ���������ʻ����ͼ��������ְ�֮��ľ���y���ף���������ʱ��x�����ӣ�֮��ĺ���ͼ����������������ʱ���ְ־��빫˾_____�ף�
���𰸡�3400��
��������
���ݺ���ͼ���֪��������10���Ӻְ��������ޣ����ݴ�ʱ�ְֵ�5���ӵ��г̵�������ǰ5���ӵ��г����5���ӵ��г̺ͣ��õ��ְֵ��ٶ������������г����ٶȵĹ�ϵ���ٸ��ݺ���ͼ���֪���ְֵ��ϵ���˾ʱ����˾�����������ľ���Ϊ9400�ף��ٸ�����֪�����������ü����������ľ��룬�ɺ���ͼ���ֿ�֪����������������ʱ��Ϊ![]() �룬�ݴ��г����̣���������ٶ���ְֵ��ٶȣ����������ý����
�룬�ݴ��г����̣���������ٶ���ְֵ��ٶȣ����������ý����
�⣺�����������г����ٶ�Ϊxm/min����ְֵ��ٶ�Ϊ��
��5x+![]() x����5��
x����5��![]() x��m/min����
x��m/min����
�ɺ���ͼ���֪����˾�����������ľ���Ϊ9400�ף�
�߹�˾λ�ڼ�������3900�ף�
������������ľ���Ϊ��9400��3900��5500���ף���
��������ã�5x+5��![]() x+��
x+��![]() ����
����![]() ��5500��
��5500��
��ã�x��200��m/min����
��ְֵ��ٶ�Ϊ��![]() ��m/min��
��m/min��
��������������ʱ���ְ־��빫˾�ľ���Ϊ��5��300+3900����![]() ����300��3400��m����
����300��3400��m����
�ʴ�Ϊ��3400��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M��0��2��Բ�ģ�4Ϊ�뾶�ġ�M��x����A��B���㣬��y����C��D���㣬����BM���ӳ�����M�ڵ�P������PC��x���ڵ�E��
��1������DMP�Ķ�����
��2������BPE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
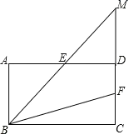
����Ŀ����ͼ�����ı���ABCD�У�AB��CD��AB��CD����A����ADC��E��F�ֱ�ΪAD��CD���е㣬����BE��BF���ӳ�BE��CD���ӳ����ڵ�M��
��1����֤���ı���ABCDΪ���Σ�
��2����MD��6��BC��12����BF�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
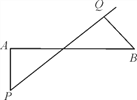
����Ŀ����ͼ��B����A�ص����������������28![]() km.A��B����֮����һ����������ĸ��ٹ�·����A��B���ص��������ٹ�·�ľ�����ȣ�����8��00���һ���ڸ��ٹ�·����ʻ������λ��A�ص����Ϸ���P����������8��20��B�ط��ָó���������������Q�����öθ��ٹ�·����Ϊ110 km/h.�ʣ��ó��Ƿ�����ʻ��
km.A��B����֮����һ����������ĸ��ٹ�·����A��B���ص��������ٹ�·�ľ�����ȣ�����8��00���һ���ڸ��ٹ�·����ʻ������λ��A�ص����Ϸ���P����������8��20��B�ط��ָó���������������Q�����öθ��ٹ�·����Ϊ110 km/h.�ʣ��ó��Ƿ�����ʻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꣬�����������ȷ��ʾ�������Сѧ���μ�����������ѧ�����ʽ���״�����˶����ܵȼ�������С�����ѧҵˮƽ���ԣ�����ѧ���ۺ�����������ϵ��Ϊ��������ѧ������ˮƽ���ƶ����ʵ�ѧ�����������ݣ�ij������ѧ�Ա�У��һ�����������꼶��ѧ������������ˮƽ��⣮Ϊ�˽�������ִ������꼶���������˲���ѧ���ļ��ɼ����������£�
���ռ����ݣ��ӳ�һ�������꼶�ֱ������ȡ��20��ѧ����ˮƽ���������������£�
��һ�꼶 | 88 | 58 | 44 | 90 | 71 | 88 | 95 | 63 | 70 | 90 |
81 | 92 | 84 | 84 | 95 | 31 | 90 | 85 | 76 | 85 | |
�����꼶 | 75 | 82 | 85 | 85 | 76 | 87 | 69 | 93 | 63 | 84 |
90 | 85 | 64 | 85 | 91 | 96 | 68 | 97 | 57 | 88 |
���������ݣ������·ֶ������������ݣ�
�ֶ� �꼶 | 0��x��60 | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
��һ�꼶 | a | 1 | 3 | 7 | b |
�����꼶 | 1 | 4 | 2 | 8 | 5 |
���������ݣ����������ݱ�������ͳ�ƣ�
ͳ���� �꼶 | ƽ���� | ��λ�� | ���� | ���� |
��һ�꼶 | 78 | c | 90 | 284.6 |
�����꼶 | 81 | 85 | d | 126.4 |
���ó����ۣ�
��1������ͳ�ƣ�������a��b��c��d��ֵ�ֱ����� ������ ������ ������ ����
��2������У��һ�������꼶��ѧ�������ֱ�Ϊ800�˺�1000�ˣ����������ο����У���һ�������ɼ�90�����ϣ���90�֣������������� ���ˣ�
��3�������������ݣ�����Ϊ�� �������һ����������ѧ������������ˮƽ�ϸߣ���˵�����ɣ�һ�����ɼ��ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
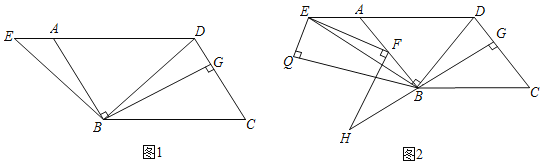
����Ŀ����ƽ���ı���ABCD�У�����BD������B��BE��BD�ڵ�B��DA���ӳ����ڵ�E������B��BG��CD�ڵ�G��
��1����ͼ1������C��60�㣬��BDC��75�㣬BD��6![]() ����AE�ij��ȣ�
����AE�ij��ȣ�
��2����ͼ2����FΪAB����һ�㣬����EF������F��FH��FE�ڵ�F��GB���ӳ����ڵ�H���ڡ�ABE����࣬��BEΪб����Rt��BEQ�����С�Q��90�㣬����QEB����BDC��EF��FH����֤��BF+BH��BQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
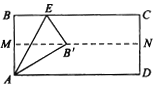
����Ŀ����ͼ��ʾ��������ABCDֽ���ۣ����ۺ�ΪMN���ٰ�B������ۺ���MN�ϣ�����ͼ��B��������![]() �����ۺ�AE�ij�Ϊ�� ��
�����ۺ�AE�ij�Ϊ�� ��
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֿ���50��ͬһ����ij�ּ�װ�䣬��ί�����乫˾�͵���ͷ�����乫˾��ÿ�ο�װ��1����2����3�����ּ�װ��������ͺŵĻ������������ͺŵĻ���ÿ���շѷֱ�Ϊ120Ԫ��160Ԫ��180Ԫ��Ҫ����20�������պ�һ��װ������Щ��װ�䣬���������ͺŵĻ���������������ж����ְ��ŷ�ʽ����Щ���ŷ�ʽ������˷����٣������˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com