
| A. | 0.1010010001 | B. | $\sqrt{9}$ | C. | $\root{3}{-64}$ | D. | $\frac{π}{2}$ |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:A、0.1010010001是有限小数,数有理数,选线错误;
B、$\sqrt{9}$=3是整数,是有理数,选项错误;
C、$\root{3}{-64}$=-4是整数,是有理数,选项错误;
D、$\frac{π}{2}$是无理数,选项错误.
故选D.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3m-n}{n+m}$ | B. | -$\frac{3m-n}{n+m}$ | C. | $\frac{m-n}{m+n}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
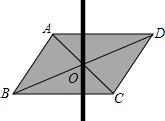 用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条
用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
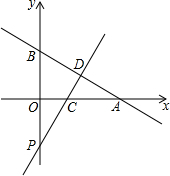 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com