
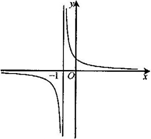
 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?| x | … | … | |||||||||||||||
| y | … | … |
分析 (1)根据函数解析式可得函数图象与直线x=3或直线x=-3没有公共点;图象与y轴的交点为(0,-2);分x<-3或-3<x<0或0<x<3或x>3讨论函数的增减性;
(2)通过列表、描点和连线化函数图象;
(3)观察函数图象得到函数y=$\frac{6}{|x|-3}$的图象关于y轴对称,而点A与点B关于y轴对称,所以a与b互为相反数;
(4)观察函数图象,找出函数值大于或等于-2所对应的自变量的值或取值范围.
解答 解:探索:(1)由数想形:函数y=$\frac{6}{|x|-3}$的图象与过点(-3,0)和(3,0)且平行于y轴的两直线没有公共点;图象与y轴的交点为(0,-2);当x<-3时,y随x的增大而增大;当-3<x<0,y随x的增大而增大;当0<x<3时,y随x的增大而减小;当x>3时,y随x的增大而减小;
(2)描点画图:
①列表:
②画图: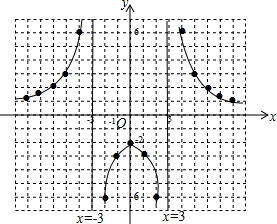
应用:(3)函数y=$\frac{6}{|x|-3}$的图象关于y轴对称,
而点A(a,c),B(b,c)为该函数图象上两对称点,
所以a+b=0;
故答案为0;
(4)当x<-3或x=0或x>3时,$\frac{6}{|x|-3}$≥-2.
点评 本题考查了反比例函数综合题:熟练掌握反比例函数图象的性质;会利用描点法画反比例函数图象.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
 图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )
图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )| A. | 体育场离早餐店4千米 | |
| B. | 张军在体育场锻炼了0.25小时 | |
| C. | 体育场离张强家2.5千米 | |
| D. | 张军从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
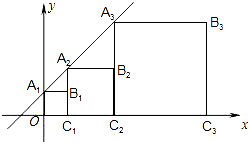 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
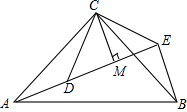 如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com