
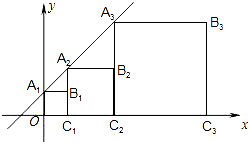
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置,点A1,A2,A3,…在直线y=x+1,点C1,C2,C3,…在x轴上,则B6的坐标是(63,32). 分析 由直线解析式可求得A1,然后分别求得B1,B2,B3…的坐标,可以得到规律:Bn(2n-1,2n-1),据此即可求解.
解答 解:
∵直线解析式是:y=x+1,
∴OA1=1
∴A1B1=1,
∴C1坐标为(1,0),
∴A2坐标为(1,2),
∴点B2的坐标为(3,2),
∴点A3的坐标为(3,4),
∴A3C2=A3B3=B3C3=4,
∴点B3的坐标为(7,4),
∴B1的纵坐标是:1=20,B1的横坐标是:1=21-1,
∴B2的纵坐标是:2=21,B2的横坐标是:3=22-1,
∴B3的纵坐标是:4=22,B3的横坐标是:7=23-1,
∴Bn的纵坐标是:2n-1,横坐标是:2n-1,
则Bn(2n-1,2n-1).
∴B6的坐标是:(26-1,26-1),即(63,32).
故答案为:(63,32).
点评 此题主要考查了待定系数法求函数解析式和坐标的变化规律.此题难度较大,注意正确得到点的坐标的规律是解题的关键


科目:初中数学 来源: 题型:选择题
| A. | a(2a+b)(a-2b) | B. | 4a(a2-2ab+b2) | C. | a(2a-b)2 | D. | 4a(a-b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
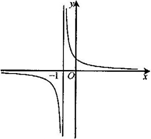
 如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )
如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
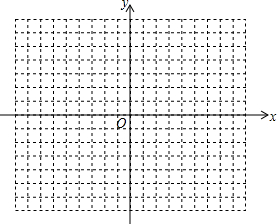
 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?| x | … | … | |||||||||||||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com