【题目】从一个等腰三角形纸片的顶角顶点出发，能将其剪成两个等腰三角形纸片，则原等腰三角形纸片的顶角等于（ ）
A.90°B.72°C.108°D.90°或108°
【答案】D
【解析】
由题意，等腰△ABC中，从顶点A出发将△ABC剪成两个三角形，则剪痕必与底边BC相交，设交于点D.
①当∠C=∠ADC时，此时∠B=∠ADC，不存在；
②当∠ADC=∠CAD时，此时∠ADB=180°-∠ADC>∠BAC-∠CAD=∠BAD，且∠B≠∠ADB，则要使△ABD为等腰三角形，只有∠B=∠BAD，如图，设∠B=x，则∠C=∠BAD=x，∠ADC=∠CAD=2x，由∠B+∠BAC+∠C=180°，则x+3x+x=180°，则x=36°，则∠BAC=3x=108°；
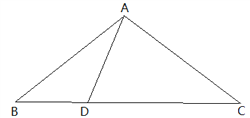
③当∠C=∠CAD时，若要使△ABD为等腰三角形，当∠B=∠BAD时，如图，此时∠B=∠BAD=∠C=∠CAD，由∠B+∠BAC+∠C=180°，则4∠B=180°，则∠B=45°，则∠BAC=90°；当∠BAD=∠ADB时，此时图形同②中成立时的情况.
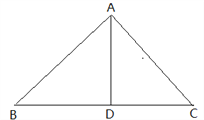
综上，∠BAC=90°或108°.
故选D.
名校通行证有效作业系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D为BC边上一点，∠1＝∠2＝∠3，AC＝AE.
求证：△ABC≌△ADE；(填空)
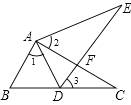
证明：∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2＝∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1＝∠2(已知)
∴∠1+∠CAD＝∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D为
的AB边上的中点，点前E为AD的中点，
为正三角形，给出下列结论，①
,②
，③
，④若
，点
是
上一动点，点到
、
边的距离分别为
，
，则
的最小值是3.其中正确的结论是_________（填写正确结论的番号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某省为推广新能源汽车，计划连续五年给予财政补贴．补贴开始时间为
年度，截止时间为
年度．补贴期间后一年度的补贴额均在前一年度补贴额基础上递增．计划前三年，每年度按固定额度
亿元递增；后两年均在上一年的基础上按相同增长率递增．已知
年度计划补贴额为
亿元．
若
年度计划补贴额比年度至少增加
，求的取值范围；
若预计
这五年补贴总额比年度补贴额的
倍还多
亿元，求后两年财政补贴的增长率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．
（1）当∠BDA=115°时，∠EDC=______°，∠AED=______°；
（2）线段DC的长度为何值时，△ABD≌△DCE，请说明理由；
（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求∠BDA的度数；若不可以，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、
、
；
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4 cm，则球的半径长是（ ）
A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
（1）（2x+y）2﹣y（2x+y），其中x＝
，y＝﹣1；
（2）[（a﹣2b）2+（a﹣2b）（a+2b）﹣2a（2a﹣b）]÷2a，其中a＝3，b＝2．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
