
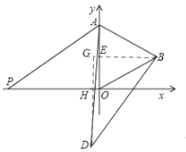
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪��AOB�ǵȱ������Σ���A�������ǣ�0��4������B�ڵ�һ���ޣ���P��x���ϵ�һ�����㣬����AP��������AOP���ŵ�A����ʱ�뷽����ת��ʹ��AO��AB�غϣ��õ���ABD��

��1����ֱ��AB�Ľ���ʽ��
��2������P�˶����㣨![]() ��0��ʱ�����ʱDP�ij�����D�����ꣻ
��0��ʱ�����ʱDP�ij�����D�����ꣻ
��3���Ƿ���ڵ�P��ʹ��OPD���������![]() �������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1������ͼ1������B��BE��y���ڵ�E����BF��x���ڵ�F��
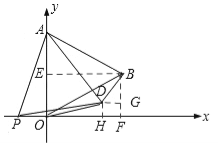
����֪�ã�BF=OE=2����![]() ��
��
����B�������ǣ�![]() ��2����
��2����
��ֱ��AB�Ľ���ʽ��y=kx+b��k��0��������
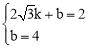 �����
�����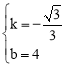 ��
��
��ֱ��AB�Ľ���ʽ��![]() ��
��
��2���ߡ�ABD����AOP��ת�õ���
���ABD�ա�AOP����AP=AD����DAB=��PAO��
���DAP=��BAO=60�������ADP�ǵȱ���������
��![]() ��
��
����ͼ2������D��DH��x���ڵ�H���ӳ�EB��DH�ڵ�G����BG��DH��
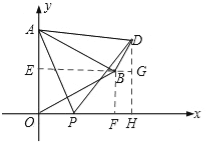
��Rt��BDG�У���BGD=90�㣬��DBG=60����
��BG=BDcos60��=![]() ��DG=BDsin60��=
��DG=BDsin60��=![]() ��
��
��OH=EG=![]() ��DH=
��DH=![]() ��
��
����D��������![]() ��
��![]() ����
����
��3�����ڡ�
������ڵ�P���������˶������У�ʹ��OPD���������![]() ��
��
���PΪ��t��0�������������������ۣ�
����t��0ʱ������ͼ2��BD=OP=t��DG=![]() t����DH=2+
t����DH=2+![]() t��
t��
�ߡ�OPD���������![]() ����
����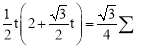 ��
��
���![]() ����ȥ����
����ȥ����
����P1��������![]() ��0����
��0����
�ڡ���D��x����ʱ�����ͼ3��

����������Ǻ������BD=OP=![]() ��
��
����![]() ��t��0ʱ������ͼ1��BD=OP=��t��DG=
��t��0ʱ������ͼ1��BD=OP=��t��DG=![]() t��
t��
��GH=BF=2����![]() t��=2+
t��=2+![]() t��
t��
�ߡ�OPD���������![]() ����
����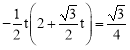 �����
�����![]() ��
��
����P2��������![]() ��0������P3��������
��0������P3��������![]() ��0����
��0����
����t��![]() ʱ������ͼ4��BD=OP=��t��DG=
ʱ������ͼ4��BD=OP=��t��DG=![]() t��
t��
��DH=![]() t��2��
t��2��
�ߡ�OPD���������![]() ��
��
��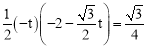 �����
�����![]() ����ȥ����
����ȥ����
����P4��������![]() ��0����
��0����
������������P������ֱ�ΪP1��![]() ��0����P2��
��0����P2��![]() ��0����P3��
��0����P3��![]() ��0����
��0����
P4��![]() ��0����
��0����
����������1������B��BE��y���ڵ�E����BF��x���ڵ�F���������BF=OE=2�����ù��ɶ������OF��Ȼ��ɵõ�B�����꣮��ֱ��AB�Ľ���ʽ��y=kx+b������֪�������������
��2������ABD����AOP��ת�õ�����ABD�ա�AOP��AP=AD����DAB=��PAO����DAP=��BAO=60�㣬��ADP�ǵȱ������������ù��ɶ������DP����Rt��BDG�У���BGD=90�㣬��DBG=60�㣮�������Ǻ������BG=BDcos60�㣬DG=BDsin60�㣮Ȼ�����OH��DH��Ȼ�������D��������
��3������������������ۣ�
����P��x����������ʱ����t��0ʱ��
����P��x�Ḻ���ᣬ��D��x���Ϸ�ʱ����![]() ��t��0ʱ
��t��0ʱ
����P��x�Ḻ���ᣬD��x���·�ʱ����t��![]() ʱ��
ʱ��
�ۺ�����������������������������t��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺̽������y=|x|��2��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y=|x|��2��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1���ں���y=|x|��2�У��Ա���x����������ʵ����
��2�������y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | 1 | 0 | ��1 | ��2 | ��1 | 0 | m | �� |
��m=�� ����
����A��n��8����B��10��8��Ϊ�ú���ͼ���ϲ�ͬ�����㣬��n=�� ����
��3����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ����
���ݺ���ͼ��ɵã�
�ٸú�������СֵΪ�� ����
����ֱ֪��![]() �뺯��y=|x|��2��ͼ����C��D���㣬��y1��yʱx��ȡֵ��Χ���� ����
�뺯��y=|x|��2��ͼ����C��D���㣬��y1��yʱx��ȡֵ��Χ���� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڰ뾶Ϊ5�ġ�O�У�AB��CD�ǻ��ഹֱ�������ң�����ΪP����AB��CD��8����OP�ij�Ϊ( )

A. 3 B. 4 C. 3![]() D. 4
D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ס��ҡ�������������������Ϸ����һ���ɼ�����������ҡ���������ijһ�ˣ��ӵڶ�����ÿһ�ζ��ɳ����߽�������������������˵�ijһ�ˣ���ڶ��δ������ص�������ĸ��ʣ�������������״ͼ�������б����ȷ�ʽ���������̣�
��2�����������n��n��2����������1��ͬ������Ϸ����ô�������δ������ص�������ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪A��3��0����B��4��4����ԭ��O��0��0����������y=ax2+bx+c ��a��0���ϣ�

��1���������ߵĽ���ʽ��
��2����ֱ��OB����ƽ��m����λ���Ⱥõ���ֱ����������ֻ��һ������D����m��ֵ����D�����꣮
��3����ͼ2������N���������ϣ�����NBO=��ABO�����ڣ�2���������£��������������POD�ס�NOB�ĵ�P�����꣨��P��O��D�ֱ����N��O��B��Ӧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��CE��BE�Ľ���ΪE���������²�����
��һ�β������ֱ�����ABE����DCE��ƽ���ߣ�����ΪE1��
�ڶ��β������ֱ�����ABE1����DCE1��ƽ���ߣ�����ΪE2��
�����β������ֱ�����ABE2����DCE2��ƽ���ߣ�����ΪE3������
��n�β������ֱ�����ABEn��1����DCEn��1��ƽ���ߣ�����ΪEn��
����En=1�ȣ�����BEC������ ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F������CF��

��1����֤��AF=DC��
��2����AB��AC�����ж��ı���ADCF����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������B����O�����ߣ��ڸ�������ȡ��C������AC����O��D������O�İ뾶��6����C=36�������ӻ�AD�ij��ǣ�������

A. ![]() B.
B. ![]() C.
C. ![]() D. 3��
D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������һЩ������������Ҫ����������������������3����������ܷ��ò�����2200Ԫ����������2500Ԫ��
��1���̳����������ۼ�Ϊ20Ԫ/����������ۼ�Ϊ50Ԫ/��������ѧУ�����ķ��ã��м��ֹ�����ÿ�ַ���������������������Ϊ���٣�
��2���ڣ�1���ķ����У���һ�ַ������ܷ������٣����ٵķ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com