
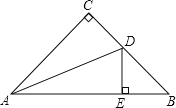
【题目】如图,在△ABC中,BC=AC,∠C=90°,AC=7cm,AD是∠BAC的平分线,交BC于D,DE⊥AB于E,求△DEB的周长.
【答案】7![]() cm.
cm.
【解析】
根据角平分线上的点到角的两边的距离相等可得CD=ED,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,然后求出△DEB的周长=AB,在等腰直角三角形ABC中由勾股定理求出AB即可得解.
∵AD是∠BAC的平分线,DE⊥AB于E,∠C=90°,
∴CD=ED,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
又∵AC=BC,
∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB,
∵在△ABC中,BC=AC,∠C=90°,AC=7cm,
∴AB=![]() cm,
cm,
∴△DEB的周长=7![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
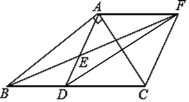
(1)判断四边形ABDF的形状,并说明理由;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在A地到B地的快速通道某隧道建设,将由甲,乙两个工程队共同施工完成,据调查得知:甲,乙两队单独完成这项上程所需天数之比为4:5,若先由甲,乙两队合作40天,剩下的工程再乙队做10天完成,
(1)求甲.乙两队单独完成这取工程各需多少天?
(2)若此项工程由甲队做m天,乙队n天完成,
①请用含m的式子表示n;
②已知甲队每天的施工费为15万元,乙队每天的施工费用为10万元,若工程预算的总费用不超过1150万元,甲队工作的天数与乙队工作的天数之和不超过90天.请问甲、乙两队各工作多少天,完成此项工程总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题2019年是决胜全面建成小康社会、打好污染防治攻坚战的关键之年.为了解决垃圾回收最后一公里的难题,“小黄狗”智能垃圾分类回收环保公益项目通过大数据、人工智能和物联网等先进科技进驻小区、写字楼、学校、机关和社区等进行回收.某位小区居民装修房屋,在过去的一个月内投放纸类垃圾和塑料垃圾共82公斤,其中纸类垃圾的投放是塑料垃圾的8倍多10公斤,请问这位小区居民在过去的一个月内投放纸类垃圾和塑料垃圾分别是多少公斤?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:有理数a、b、c在数轴上的位置如图所示,且|c|>|a|.
![]()
(1)若|a+10|=20,b2=400,c的相反数是30,求a、b、c的值;
(2)在(1)的条件下,a、b、c分别是A、B、C点在数轴上所对应的数,
①线段AC的长是________,将数轴折叠使得点A和点C重合,则折痕处在数轴上表示的数是__________
②数轴上是否存在一点P,使得P点到C点的距离加上P点到A点的距离减去P点到B点的距离为50,即PC+PAPB=50?若存在,求出P点在数轴上所对应的数;若不存在,请说明理由;
③点C,B分别以4个单位/秒和3个单位/秒的速度同时向右运动,点A以7个单位/秒的速度向右运动,是否存在常数m,使得3CA+2mOB-mOA为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历

(1)如图1,带阴影的方框中的9个数的和与方框中心的数有什么关系?并试着说明理由;
(2)如果将阴影的方框移至图2的位置,(1)中关系的关系还成立吗?并试着说明理由;
(3)不改变阴影方框的大小,将方框移动几个位置试一试,你能得出什么结论?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
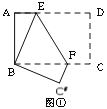
【题目】(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点![]() 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么![]() 的度数为 。
的度数为 。
(2)观察发现:
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.

(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com