
【题目】(1)动手操作:
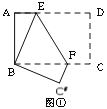
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点![]() 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么![]() 的度数为 。
的度数为 。
(2)观察发现:
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.

(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。

【答案】(1)125°;(2)同意;(3)60°
【解析】
试题分析:(1)先根据矩形的性质结合三角形的内角和定理求得∠AEB的度数,再根据折叠的性质求得∠DEF的度数,然后根据平行线的性质求得∠EFC的度数,即可得到结果;
(2) 设AD与EF交于点G.由折叠的性质可得AD平分∠BAC,所以∠BAD=∠CAD.∠AGE=∠DGE=90°,即得∠AEF=∠AFE,从而可以证得结论;
(3)过N作NH⊥AD于H,设![]() ,根据折叠的性质及勾股定理可证得△MPF为等边三角形,则∠MFE=30°,∠MFN=60°,又MN=MF=
,根据折叠的性质及勾股定理可证得△MPF为等边三角形,则∠MFE=30°,∠MFN=60°,又MN=MF=![]() ,则△MNF为等边三角形,即可求得结果;
,则△MNF为等边三角形,即可求得结果;
(1)因为∠ABE=20°,所以∠AEB=70°
由折叠知,∠DEF=55°
所以![]() =∠EFC=125°;
=∠EFC=125°;
(2)同意.
设AD与EF交于点G.

由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
由折叠知,∠AGE=∠DGE=90°,
所以∠AGE=∠AGF=90°,
所以∠AEF=∠AFE.所以AE=AF,
即△AEF为等腰三角形.
(3)过N作NH⊥AD于H

设![]()
由折叠知,![]() ①
①
![]()
 ②
②
![]()
∴△MPF为等边三角形
∴∠MFE=30°
∴∠MFN=60°,
又∵MN=MF=![]()
∴△MNF为等边三角形
∴∠MNF=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
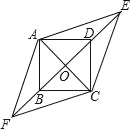
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
A. DE=1 B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=![]() .
.
(1)求双曲线和和直线的解析式.
(2)求△AOB的面积.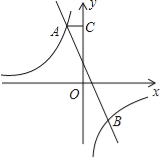
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
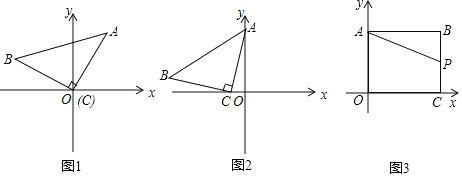
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
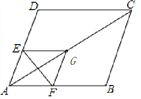
【题目】如图在菱形ABCD中,∠A=60°,AD=![]() ,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
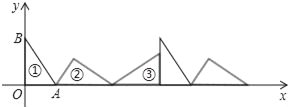
【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com