练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE=，∠EAF=135°，则以下结论正确的是（　　）

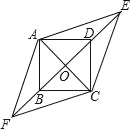
    A. DE=1 B. tan∠AFO= C. AF= D. 四边形AFCE的面积为

    【答案】C

    【解析】因为四边形ABCD是正方形,所以AB=CB=CD=AD=1,AC⊥BA, ∠ADO=∠ABO=45°,所以OD=OB=OA=, ∠ABF=∠ADE=135°,在Rt△AEO中,根据勾股定理可得:EO=,DE=,所以A错误,因为∠EAF =135°, ∠BAD =90°,所以∠EAF =135°,

    ∠BAF+∠DAE=45°, 所以∠BAF =∠AED, 所以△ABF ∽△EDA ,所以,,所以BF=,Rt△AOF中,由勾股定理可得:AF=,所以C正确,所以tan∠AFO=,所以B错误,所以,所以D错误,故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在A地到B地的快速通道某隧道建设，将由甲，乙两个工程队共同施工完成，据调查得知：甲，乙两队单独完成这项上程所需天数之比为4：5，若先由甲，乙两队合作40天，剩下的工程再乙队做10天完成，

    （1）求甲．乙两队单独完成这取工程各需多少天？

    （2）若此项工程由甲队做m天，乙队n天完成，

    ①请用含m的式子表示n；

    ②已知甲队每天的施工费为15万元，乙队每天的施工费用为10万元，若工程预算的总费用不超过1150万元，甲队工作的天数与乙队工作的天数之和不超过90天．请问甲、乙两队各工作多少天，完成此项工程总费用最少？最少费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的中心，则阴影部分的面积是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某月的月历

    （1）如图1，带阴影的方框中的9个数的和与方框中心的数有什么关系？并试着说明理由；

    （2）如果将阴影的方框移至图2的位置，（1）中关系的关系还成立吗？并试着说明理由；

    （3）不改变阴影方框的大小，将方框移动几个位置试一试，你能得出什么结论？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一副直角三角板（其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°）

    （1）如图①放置，AB⊥AD,∠CAE=_______，BC与AD的位置关系是__________；

    （2）在（1）的基础上，再拿一个30°,60°,90°的直角三角板，如图②放置，将AC′边和AD边重合， AE是∠CAB′的角平分线吗，如果是，请加以说明，如果不是，请说明理由．

    （3）根据（1）（2）的计算，请解决下列问题：

    如图③∠BAD=90°，∠BAC=∠FAD= （是锐角），将一个45°,45°,90°直角三角板的一直角边与AD边重合，锐角顶点A与∠BAD的顶点重合，AE是∠CAF的角平分线吗？如果是，请加以说明，如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在菱形中，,点是射线上一动点，以为边向右侧作等边，点的位置随点的位置变化而变化.

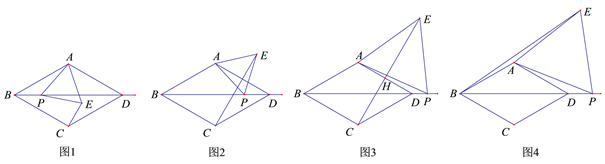
    （1）如图1，当点在菱形内部或边上时，连接，与的数量关系是 ，与的位置关系是 ；

    （2）当点在菱形外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，

    请说明理由(选择图2，图3中的一种情况予以证明或说理).

    (3) 如图4，当点在线段的延长线上时，连接，若 , ,求四边形的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD 是△ABC 的角平分线，DE，DF 分别是△BAD 和△ACD 的高，得到下列四个结论：①OA＝OD；②AD⊥EF；③当∠A＝90°时，四边形 AEDF 是正方形；④AE+DF＝AF+DE．其中正确的是_________（填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）动手操作：

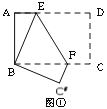
    如图①，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点处，折痕为EF，若∠ABE=20°，那么的度数为 。

    （2）观察发现：

    小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．

    （3）实践与运用：

    将矩形纸片ABCD 按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP=MN=PQ（如图④）,求∠MNF的大小。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

    （1）数轴上点B表示的数是　 　，点P表示的数是　 　（用含t的代数式表示）；

    （2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发．求：

    ①当点P运动多少秒时，点P与点Q相遇？

    ②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

    查看答案和解析>>

    同步练习册答案