
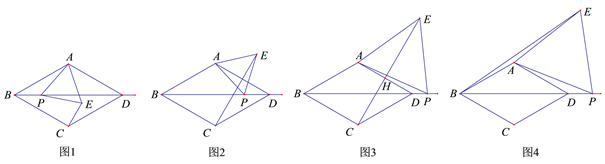
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)BP=CE; CE⊥AD;(2)成立,理由见解析;(3)![]() .
.
【解析】(1)①连接AC,证明△ABP≌△ACE,根据全等三角形的对应边相等即可证得BP=CE;②根据菱形对角线平分对角可得![]() ,再根据△ABP≌△ACE,可得
,再根据△ABP≌△ACE,可得![]() ,继而可推导得出
,继而可推导得出![]() ,即可证得CE⊥AD;
,即可证得CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,利用(1)的方法进行证明即可;
(3)连接AC交BD于点O,CE,作EH⊥AP于H,由已知先求得BD=6,再利用勾股定理求出CE的长,AP长,由△APE是等边三角形,求得![]() ,
, ![]() 的长,再根据
的长,再根据![]() ,进行计算即可得.
,进行计算即可得.
(1)①BP=CE,理由如下:
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE ,∠PAE=60° ,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE;
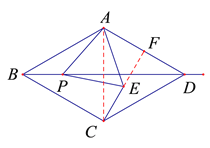
②CE⊥AD ,
∵菱形对角线平分对角,
∴![]() ,
,
∵△ABP≌△ACE,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CF⊥AD ,即CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,理由如下:
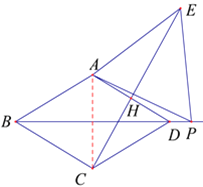
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
∴AB=AC,∠BAD=120° ,
∠BAP=120°+∠DAP,
∵△APE是等边三角形,
∴AP=AE , ∠PAE=60° ,
∴∠CAE=60°+60°+∠DAP=120°+∠DAP,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE,![]() ,
,
∴∠DCE=30° ,∵∠ADC=60°,
∴∠DCE+∠ADC=90° , ∴∠CHD=90° ,∴CE⊥AD,
∴(1)中的结论:BP=CE,CE⊥AD 仍然成立;
(3) 连接AC交BD于点O,CE,作EH⊥AP于H,
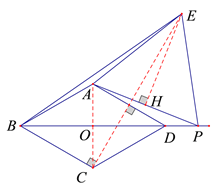
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC ,
∵∠ABC=60°,![]() ,
,
∴∠ABO=30° ,∴![]() , BO=DO=3,
, BO=DO=3,
∴BD=6,
由(2)知CE⊥AD,
∵AD∥BC,∴CE⊥BC,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
由(2)知BP=CE=8,∴DP=2,∴OP=5,
∴![]() ,
,
∵△APE是等边三角形,∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
=![]()
=![]()
=![]() ,
,
∴四边形ADPE的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多![]() 小时,求自行车的平均速度?
小时,求自行车的平均速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
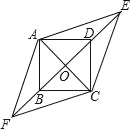
A. DE=1 B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=![]() .
.
(1)求双曲线和和直线的解析式.
(2)求△AOB的面积.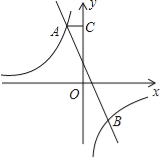
查看答案和解析>>
科目:初中数学 来源: 题型:
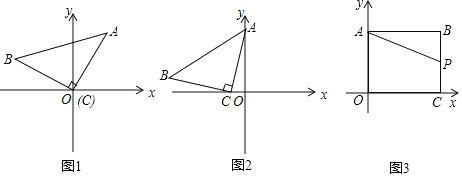
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com