
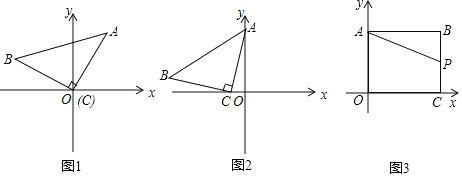
����Ŀ��![]() ����˼������ͼ1����ƽ��ֱ������ϵ�У�����
����˼������ͼ1����ƽ��ֱ������ϵ�У�����![]() ��ֱ�Ƕ���C��ԭ�㣬�������ŵ�O��ת��������Aǡ�����ڵ�
��ֱ�Ƕ���C��ԭ�㣬�������ŵ�O��ת��������Aǡ�����ڵ�![]() ��
��![]() ��
��![]() �ij�Ϊ______��
�ij�Ϊ______��![]() ��B������Ϊ______
��B������Ϊ______![]() ֱ��д���
ֱ��д���![]()
![]() ����Ӧ�ã���ͼ2����ƽ��ֱ������ϵ�У�������
����Ӧ�ã���ͼ2����ƽ��ֱ������ϵ�У�������![]() ��ͼ���ã�ֱ�Ƕ���
��ͼ���ã�ֱ�Ƕ���![]() ����
����![]() ������ֱ��AB�ĺ�������ʽ��
������ֱ��AB�ĺ�������ʽ��
![]() ��չ�о�����ͼ3����ֱ������ϵ�У���
��չ�о�����ͼ3����ֱ������ϵ�У���![]() ������B��
������B��![]() �ᣬ����Ϊ��A����
�ᣬ����Ϊ��A����![]() �ᣬ����Ϊ��C��P���߶�BC�ϵ�һ�����㣬��Q��ֱ��
�ᣬ����Ϊ��C��P���߶�BC�ϵ�һ�����㣬��Q��ֱ��![]() ��һ����
��һ����![]() ���Ƿ�����Ե�PΪֱ�Ƕ���ĵ���
���Ƿ�����Ե�PΪֱ�Ƕ���ĵ���![]() �������ڣ��������ʱP�����꣬�������ڣ���˵�����ɣ�
�������ڣ��������ʱP�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��![]() ��
��![]() ��2��
��2��![]() ��3��
��3��![]() ��
��![]()
��������
![]() ��
��![]() �ɵã�
�ɵã�![]() ��
��![]() ��
��![]() ����֤
����֤![]() ��
��![]() ��
��![]() ��
��![]() �����
�����![]() ��
��
![]() ͬ
ͬ![]() ��֤
��֤![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����
�����![]() ���������һ�κ�������ʽ���ɣ�
���������һ�κ�������ʽ���ɣ�
![]() �������������
�������������![]() ����Q��x���·�ʱ��
����Q��x���·�ʱ��![]() ����Q��x���Ϸ�ʱ
����Q��x���Ϸ�ʱ![]() ���ݵ���
���ݵ���![]() ����һ����ֱ�ǣ��Ӷ���⣮
����һ����ֱ�ǣ��Ӷ���⣮
![]() ��ͼ1����
��ͼ1����![]() �ᣬ
�ᣬ![]() �ᣮ
�ᣮ
![]() ��
��
![]() ��
��![]() ��
��![]()
![]() ��
��![]()
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��
![]() ��ͼ2������B��
��ͼ2������B��![]() �ᣮ
�ᣮ
![]() ��
��![]()
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]()
![]() ��
��
��ֱ��AB�ı���ʽΪ![]()
��![]() ��
��![]() ���룬��
���룬��
![]() ��
��
���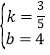 ��
��
![]() ֱ��AB�ĺ�������ʽ
ֱ��AB�ĺ�������ʽ![]() ��
��
![]() ��ͼ3����
��ͼ3����![]() �������������
�������������
![]() ����Q��x���·�ʱ��
����Q��x���·�ʱ��![]() �ᣬ��BP���ӳ��߽��ڵ�
�ᣬ��BP���ӳ��߽��ڵ�![]() ��
��
![]() ��
��
![]() ��
��
![]()
��![]() ��
��![]() ��
��
![]() ��
��![]()
![]() ��
��![]()
![]() ��
��![]() ��
��
![]()
![]() ��
��
���![]()
![]()
��ʱ��P���C�غϣ�
![]() ��
��
![]() ����Q��x���Ϸ�ʱ��
����Q��x���Ϸ�ʱ��![]() �ᣬ��PB���ӳ��߽��ڵ�
�ᣬ��PB���ӳ��߽��ڵ�![]() ��
��
ͬ����֤![]() ��
��![]() ��
��
ͬ�����![]()
���ϣ�P������Ϊ��![]() ��
��![]()


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ķ���B��C��x����������ϣ�����������y= ![]() ��k��0���ڵ�һ����ͼ������A��m��2����CD���ϵĵ�E��n��
��k��0���ڵ�һ����ͼ������A��m��2����CD���ϵĵ�E��n�� ![]() ��������E��ֱ��l��x���ڵ�F����y���ڵ�G��0����2�������F�������� ��
��������E��ֱ��l��x���ڵ�F����y���ڵ�G��0����2�������F�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ����
����![]() ����P��ֱ��
����P��ֱ��![]() ��һ�㣬��
��һ�㣬��![]() �����P������Ϊ______��
�����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[��ѧʵ��̽���]
ʵ������������ɿ���ͼ����ʾ�������κͳ�����ӲֽƬ��

ʵ��Ŀ�ģ�
�����ɿ������������κͳ�����ӲֽƬƴ��һ���µij����Σ�ͨ����ͬ�ķ�������������õ���Ӧ�ĵ�ʽ���Ӷ�̽�������ʽ�˷���ֽ���ʽ����;����
���磬ѡȡ�����Ρ�������ӲֽƬ�� 6 �飬ƴ��һ����ͼ�ڵij����Σ�������������� д����Ӧ�ĵ�ʽ�� a2+3ab+2b2=(a+2b)(a+b)�� (a+2b)(a+b) =a2+3ab+2b2��
����̽����
(1) С������ƴͼ�ķ������Ͷ���ʽ�˷�(2a+b)(a+b) =2a2+3ab+b2 ����ô��Ҫ����������ֽƬ �ţ�������ֽƬ �ţ�
(2)ѡȡ�����Ρ�������ӲֽƬ�� 8 �飬����ƴ��һ����ͼ�۵ij����Σ�����ͼ�۵��������д����Ӧ�ĵ�ʽ��
(3)�Խ���ƴͼ�ķ������Ѷ�������ʽ 2a2+5ab+2b2 �ֽ���ʽ��������ƴ��ͼ�λ������߷�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1����![]() ����3��20160��|��5|��
����3��20160��|��5|��
��2����3a2��2��a22a2+����2a3��2+a2��
��3����x+5��2����x��2����x��3����
��4����2x+y��2����2x+y+2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������p��y=ax2+bx+c�Ķ���ΪC����x���ཻ��A��B���㣨��A�ڵ�B��ࣩ����C����x��ĶԳƵ�ΪC�䣬���dz���AΪ�����ҹ���C�䣬�Գ�����y��ƽ�е�������Ϊ������p�ġ���֮�ǡ������ߣ�ֱ��AC��Ϊ������p�ġ���֮�ǡ�ֱ�ߣ���һ�������ߵġ���֮�ǡ������ߺ͡���֮�ǡ�ֱ�߷ֱ���y=x2+2x+1��y=2x+2�������������ߵĽ���ʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������μ����е���̨��֯�ġ�ĵ���������������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ��������������ᣬ���������������������������ã�ʹ�á�������һ�ο�����������ȥ������һ���һ������ѡ���
��1������������Ρ����������ڵ�һ������ʹ�ã���ô����ͨ�صĸ����� ��
��2������������Ρ����������ڵڶ�������ʹ�ã���ô����ͨ�صĸ����� ��
��3���������ÿ�������һ�Ρ���������������״ͼ�����б���������˳��ͨ�صĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����м���ԭ��130kg������ԭ��144kg������������ԭ��������A��B���ֲ�Ʒ��30������֪����ÿ��A��Ʒ�����ԭ��5kg������ԭ��4kg����ÿ��A��Ʒ�ɻ���700Ԫ������ÿ��B��Ʒ�����ԭ��3kg������ԭ��6kg����ÿ��B��Ʒ�ɻ���900Ԫ��������A��Ʒx��(��Ʒ����Ϊ������)������������Ϣ����������⣺
��1������A��B���ֲ�Ʒ�ķ������ļ��֣�
��2��д����1�����������ķ�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ƽ����AE��CF���ڵ�P��BD�ǡ�ABC�ĸߣ���H��AC�ϣ�AF��AH�����н��ۣ�����APC��90��+![]() ABC����PHƽ�֡�APC������BC��AB������BP�����DBP����BAC����BCA������PH��BD�����ABCΪ���������Σ�������ȷ�Ľ�����_____������ţ���
ABC����PHƽ�֡�APC������BC��AB������BP�����DBP����BAC����BCA������PH��BD�����ABCΪ���������Σ�������ȷ�Ľ�����_____������ţ���
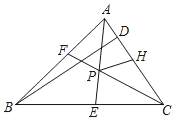
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com