
【题目】如图,△ABC角平分线AE、CF交于点P,BD是△ABC的高,点H在AC上,AF=AH,下列结论:①∠APC=90°+![]() ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
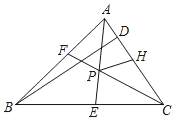
【答案】①④.
【解析】
①利用三角形的内角和定理以及角平分线的定义即可判断.
②利用反证法进行判断.
③根据∠DBP=∠DBC﹣∠PBC=90°﹣∠ACB﹣![]() (180°﹣∠BAC﹣∠ACB)=
(180°﹣∠BAC﹣∠ACB)=![]() (∠BAC﹣∠ACB),由此即可判断.
(∠BAC﹣∠ACB),由此即可判断.
④利用全等三角形的性质证明CA=CB即可判断.
解:∵△ABC角平分线AE、CF交于点P,
∴∠CAP=![]() ∠BAC,∠ACP=
∠BAC,∠ACP=![]() ∠ACB,
∠ACB,
∴∠APC=180°﹣(∠CAP+∠ACP)=180°﹣![]() (∠BAC+∠ACB)=180°﹣
(∠BAC+∠ACB)=180°﹣![]() (180°﹣∠ABC)=90°+
(180°﹣∠ABC)=90°+![]() ∠ABC,故①正确,
∠ABC,故①正确,
∵PA=PA,∠PAF=∠PAH,AF=AH,
∴△PAF≌△PAH(SAS),
∴∠APF=∠APH,
若PH是∠APC的平分线,则∠APF=60°,显然不可能,故②错误,
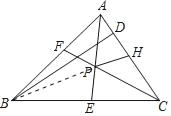
∵∠DBP=∠DBC﹣∠PBC=90°﹣∠ACB﹣![]() (180°﹣∠BAC﹣∠ACB)=
(180°﹣∠BAC﹣∠ACB)=![]() (∠BAC﹣∠ACB),故③错误,
(∠BAC﹣∠ACB),故③错误,
∵BD⊥AC,PH∥BD,
∴PH⊥AC,
∴∠PHA=∠PFA=90°,
∵∠ACF=∠BCF,CF=CF,∠CFA=∠CFB=90°,
∴△CFA≌△CFB(ASA),
∴CA=CB,故④正确,
故答案为①④.


科目:初中数学 来源: 题型:
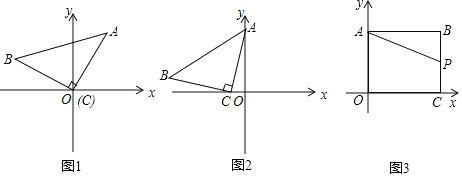
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.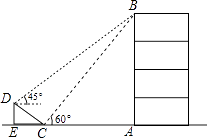
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB= ![]() ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.
(1)求直线l的表达式;
(2)若反比例函数y= ![]() 的图象经过点P,求m的值.
的图象经过点P,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )

A. 13B. 16C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
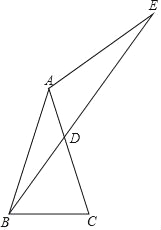
【题目】如图,已知△ABC中AB=AC,在AC上有一点D,连接BD,并延长至点E,使AE=AB.
(1)画图:作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠ABE=∠ACF;
(3)若AC=8,∠E=15°,求三角形ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°.
(1)用直尺和圆规作∠A的平分线交 BC 于点 P(保留作图的痕迹,不写作法);
(2)当∠CAB为 度时,点 P 到 A,B 两点的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、"10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com