
【题目】如图,在 Rt△ABC 中,∠ACB=90°.
(1)用直尺和圆规作∠A的平分线交 BC 于点 P(保留作图的痕迹,不写作法);
(2)当∠CAB为 度时,点 P 到 A,B 两点的距离相等.

科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
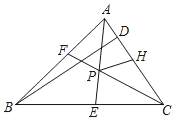
【题目】如图,△ABC角平分线AE、CF交于点P,BD是△ABC的高,点H在AC上,AF=AH,下列结论:①∠APC=90°+![]() ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=90°,AB=8,CB=5,动点M从C点开始沿CB运动,动点N从B点开始沿BA运动,同时出发,两点均以1个单位/秒的速度匀速运动(当M运动到B点即同时停止),运动时间为t秒.
(1)AN= ;CM= .(用含t的代数式表示)
(2)连接CN,AM交于点P.
①当t为何值时,△CPM和△APN的面积相等?请说明理由.
②当t=3时,试求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AD,CB=CE.
(1)当∠ABC=90°时(如图①),∠EBD= °;
(2)当∠ABC=n°(n≠90)时(如图②),求∠EBD 的度数(用含 n 的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=BC,点F是AB的中点,点E是BC边上的点,DE=AD+BE,△DEF 的周长为l.
(1)求证:DF 平分∠ADE;
(2)若 FD=FC,AB=2,AD=3,求l的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字,并完成证明;
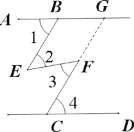
已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;
证明:如图,延长CF交AB于点G
∵∠2=∠3
∴BE∥CF( )
∴∠1= ( )
又∠1=∠4
∴∠4= ( )
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别过反比例函数y= ![]() 的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)
的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com