
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃН8ЃЌCBЃН5ЃЌЖЏЕуMДгCЕуПЊЪМбиCBдЫЖЏЃЌЖЏЕуNДгBЕуПЊЪМбиBAдЫЖЏЃЌЭЌЪБГіЗЂЃЌСНЕуОљвд1ИіЕЅЮЛ/УыЕФЫйЖШдШЫйдЫЖЏЃЈЕБMдЫЖЏЕНBЕуМДЭЌЪБЭЃжЙЃЉЃЌдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉANЃНЁЁ ЁЁЃЛCMЃНЁЁ ЁЁЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉСЌНгCNЃЌAMНЛгкЕуPЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌЁїCPMКЭЁїAPNЕФУцЛ§ЯрЕШЃПЧыЫЕУїРэгЩЃЎ
ЂкЕБtЃН3ЪБЃЌЪдЧѓЁЯAPNЕФЖШЪ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ8ЉtЃЌtЃЛЃЈ2ЃЉЂй![]() ЃЛЂкЁЯAPNЃН45Ёу
ЃЛЂкЁЯAPNЃН45Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнТЗГЬЃНЫйЖШЁСЪБМфЃЌПЩгУКЌtЕФДњЪ§ЪНБэЪОBNЃЌCMЕФГЄЃЌМДПЩгУКЌtЕФДњЪ§ЪНБэЪОANЕФГЄЃЛ
ЃЈ2ЃЉЂйгЩЬтвтПЩЕУSЁїABMЃНSЁїBNCЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩЧѓtЕФжЕЃЛ
ЂкЙ§ЕуPзїPFЁЭBCЃЌPGЁЭABЃЌЙ§ЕуAзїAEЁЭCNЃЌНЛCNЕФбгГЄЯпгкЕуEЃЌСЌНгBPЃЌПЩжЄЫФБпаЮPGBFЪЧОиаЮЃЌПЩЕУPFЃНBGЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУЗНГЬзщЃЌЧѓГіPGЃЌPFЕФГЄЃЌИљОнЙДЙЩЖЈРэПЩЧѓPNЕФГЄЃЌЭЈЙ§жЄЁїANEЁзЁїCNBЃЌПЩЧѓAEЃЌNEЕФГЄЃЌМДПЩЧѓЁЯAPNЕФЖШЪ§ЃЎ
НтЃКЃЈ1ЃЉЁпMЃЌNСНЕуОљвд1ИіЕЅЮЛ/УыЕФЫйЖШдШЫйдЫЖЏЃЌ
ЁрCMЃНBNЃНtЃЌ
ЁрANЃН8ЉtЃЌ
ЙЪД№АИЮЊЃК8ЉtЃЌtЃЛ
ЃЈ2ЃЉЂйШєЁїCPMКЭЁїAPNЕФУцЛ§ЯрЕШ
ЁрSЁїCPM+SЫФБпаЮBMPNЃНSЁїAPN+SЫФБпаЮBMPNЃЌ
ЁрSЁїABMЃНSЁїBNCЃЌ
Ёр![]() ,
,
Ёр8ЁСЃЈ5ЉtЃЉЃН5t
ЁрtЃН![]()
ЁрЕБtЃН![]() ЪБЃЌЁїCPMКЭЁїAPNЕФУцЛ§ЯрЕШЃЛ
ЪБЃЌЁїCPMКЭЁїAPNЕФУцЛ§ЯрЕШЃЛ
ЂкШчЭМЃЌЙ§ЕуPзїPFЁЭBCЃЌPGЁЭABЃЌЙ§ЕуAзїAEЁЭCNЃЌНЛCNЕФбгГЄЯпгкЕуEЃЌСЌНгBPЃЌ

ЁпPGЁЭABЃЌPFЁЭBCЃЌЁЯBЃН90ЁуЃЌ
ЁрЫФБпаЮPGBFЪЧОиаЮЃЌ
ЁрPFЃНBGЃЌ
ЁпtЃН3ЃЌ
ЁрCMЃН3ЃНBNЃЌ
ЁрBMЃН2ЃЌANЃН5ЃЌ
ЁпSЁїABMЃНSЁїABP+SЁїBPMЃЌ
Ёр![]()
Ёр16ЃН8PG+2PFЂй
ЁпSЁїBCNЃНSЁїBCP+SЁїBPNЃЌ
Ёр![]() ЁС5ЁС3ЃН
ЁС5ЁС3ЃН![]()
Ёр15ЃН3PG+5PFЂк
гЩЂйЂкзщГЩЗНГЬзщНтЕУЃКPGЃН![]() ЃЌPFЃН
ЃЌPFЃН![]() ЃЌ
ЃЌ
ЁрBGЃН![]()
ЁрNGЃНBNЉBGЃН3Љ![]() ЃН
ЃН![]()
дкRtЁїPGNжаЃЌPNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
дкRtЁїBCNжаЃЌCNЃН![]() ЃН
ЃН![]()
ЁпЁЯBЃНЁЯEЃН90ЁуЃЌЁЯANEЃНЁЯBNC
ЁрЁїANEЁзЁїCNB
Ёр![]()
Ёр![]()
ЁрAEЃН![]() ЃЌNEЃН
ЃЌNEЃН![]()
ЁпPEЃНEN+PN
ЁрPEЃН![]() +
+![]() ЃН
ЃН![]()
ЁрAEЃНPEЃЌЧвAEЁЭPE
ЁрЁЯAPNЃН45Ёу



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЯ1+ЁЯ2=180ЁуЃЌЁЯDAE=ЁЯBCFЃЌDAЦНЗжЁЯBDFЃЎ
ЃЈ1ЃЉAEгыFCЛсЦНааТ№ЃПЫЕУїРэгЩЃЎ
ЃЈ2ЃЉADгыBCЕФЮЛжУЙиЯЕШчКЮЃПЮЊЪВУДЃП
ЃЈ3ЃЉBCЦНЗжЁЯDBEТ№ЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮ![]() ЕФЖЅЕуCгыдЕуOжиКЯЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌЕуAдкЗДБШР§КЏЪ§
ЕФЖЅЕуCгыдЕуOжиКЯЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌЕуAдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЕуDЕФзјБъЮЊ
ЕФЭМЯѓЩЯЃЌЕуDЕФзјБъЮЊ![]() ЃЎНЋСтаЮABCDбиxжсе§ЗНЯђЦНвЦ____ИіЕЅЮЛ,ПЩвдЪЙСтаЮЕФСэвЛИіЖЅЕуЧЁКУТфдкИУКЏЪ§ЭМЯѓЩЯЃЎ
ЃЎНЋСтаЮABCDбиxжсе§ЗНЯђЦНвЦ____ИіЕЅЮЛ,ПЩвдЪЙСтаЮЕФСэвЛИіЖЅЕуЧЁКУТфдкИУКЏЪ§ЭМЯѓЩЯЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќЁїABCЕФжмГЄЮЊ21ЃЌЕзБпBCЃН5ЃЌABЕФДЙжБЦНЗжЯпDEНЛABгкЕуDЃЌНЛACгкЕуEЃЌдђЁїBECЕФжмГЄЮЊЃЈЁЁЁЁЃЉ

A. 13B. 16C. 8D. 10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+2xЉ3гыxжсНЛгкAЁЂBСНЕуЃЌЧвBЃЈ1ЃЌ0ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЕуAЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЪЧжБЯпy=xЩЯЕФЖЏЕуЃЌЕБжБЯпy=xЦНЗжЁЯAPBЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌвбжЊжБЯпy= ![]() xЉ
xЉ ![]() ЗжБ№гыxжсЁЂyжсНЛгкCЁЂFСНЕуЃЌЕуQЪЧжБЯпCFЯТЗНЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуQзїyжсЕФЦНааЯпЃЌНЛжБЯпCFгкЕуDЃЌЕуEдкЯпЖЮCDЕФбгГЄЯпЩЯЃЌСЌНгQEЃЎЮЪЃКвдQDЮЊбќЕФЕШбќЁїQDEЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧыЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЗжБ№гыxжсЁЂyжсНЛгкCЁЂFСНЕуЃЌЕуQЪЧжБЯпCFЯТЗНЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуQзїyжсЕФЦНааЯпЃЌНЛжБЯпCFгкЕуDЃЌЕуEдкЯпЖЮCDЕФбгГЄЯпЩЯЃЌСЌНгQEЃЎЮЪЃКвдQDЮЊбќЕФЕШбќЁїQDEЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧыЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк RtЁїABC жаЃЌЁЯACBЃН90ЁуЃЎ
ЃЈ1ЃЉгУжБГпКЭдВЙцзїЁЯAЕФЦНЗжЯпНЛ BC гкЕу PЃЈБЃСєзїЭМЕФКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЃЈ2ЃЉЕБЁЯCABЮЊ ЖШЪБЃЌЕу P ЕН AЃЌB СНЕуЕФОрРыЯрЕШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() гыxжсКЭ y жсЗжБ№НЛгыAЃЌB СНЕуЃЌСэвЛжБЯпОЙ§ЕуBКЭЕуCЃЈ6ЃЌЃ5ЃЉЃЎ
гыxжсКЭ y жсЗжБ№НЛгыAЃЌB СНЕуЃЌСэвЛжБЯпОЙ§ЕуBКЭЕуCЃЈ6ЃЌЃ5ЃЉЃЎ
ЃЈ1ЃЉЧѓ AЃЌB СНЕуЕФзјБъЃЛ
ЃЈ2ЃЉжЄУїЃКЁїABC ЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉдк x жсЩЯеввЛЕу PЃЌЪЙЁїBCP ЪЧвд BC ЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧѓГі P ЕузјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§ЕуA0ЃЈ1ЃЌ0ЃЉзїxжсЕФДЙЯпЃЌНЛжБЯпlЃКyЃН2xгкB1ЃЌдкxжсЩЯШЁЕуA1ЃЌЪЙOA1ЃНOB1ЃЌЙ§ЕуA1зїxжсЕФДЙЯпЃЌНЛжБЯпlгкB2ЃЌдкxжсЩЯШЁЕуA2ЃЌЪЙOA2ЃНOB2ЃЌЙ§ЕуA2зїxжсЕФДЙЯпЃЌНЛжБЯпlгкB3ЃЌЁЃЌетбљвРДЮзїЭМЃЌдђЕуB8ЕФзнзјБъЮЊЃЈЁЁЁЁЃЉ
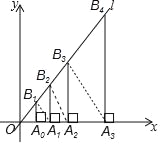
A. ЃЈ![]() ЃЉ7B. 2ЃЈ
ЃЉ7B. 2ЃЈ![]() ЃЉ7C. 2ЃЈ
ЃЉ7C. 2ЃЈ![]() ЃЉ8D. ЃЈ
ЃЉ8D. ЃЈ![]() ЃЉ9
ЃЉ9
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїDEBжаЃЌвбжЊAB=DEЃЌЛЙашЬэМгСНИіЬѕМўВХФмЪЙЁїABCЁеЁїDECЃЌВЛФмЬэМгЕФвЛзщЬѕМўЪЧ

AЃЎBC=ECЃЌЁЯB=ЁЯE BЃЎBC=ECЃЌAC=DC
CЃЎBC=DCЃЌЁЯA=ЁЯD DЃЎЁЯB=ЁЯEЃЌЁЯA=ЁЯD
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com