
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.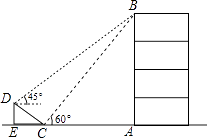
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
【答案】
(1)解:在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,
∴DE= ![]() DC=2米
DC=2米
(2)解:过D作DF⊥AB,交AB于点F,
∵∠BFD=90°,∠BDF=45°,
∴∠BFD=45°,即△BFD为等腰直角三角形, 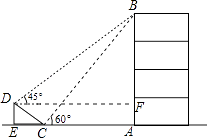
设BF=DF=x米,
∵四边形DEAF为矩形,
∴AF=DE=2米,即AB=(x+2)米,
在Rt△ABC中,∠ABC=30°,
∴BC= ![]() =
= ![]() =
= ![]() =
= ![]() 米,
米,
BD= ![]() BF=
BF= ![]() x米,DC=4米,
x米,DC=4米,
∵∠DCE=30°,∠ACB=60°,
∴∠DCB=90°,
在Rt△BCD中,根据勾股定理得:2x2= ![]() +16,
+16,
解得:x=4+4 ![]() ,
,
则AB=(6+4 ![]() )米.
)米.
【解析】解直角三角形的基本思路是把特殊角或已知角放在直角三角形中,利用三角函数得出边之间的关系,最后根据勾股定理列出方程.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励该校在南山区第二届学生技能大赛中表现突出的20名同学,派李老师为这些同学购买奖品,要求每人一件,李老师到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求笔记本和钢笔的单价分别为多少元?
(2)售货员提示,购买笔记本没有优惠:买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>10)支钢笔,所需费用为y元,请你求出y与x之间的函数关系式;
(3)在(2)的条件下,如果买同一种奖品,请你帮忙计算说明,买哪种奖品费用更低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x满足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;② ![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣ ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
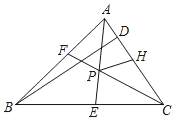
【题目】如图,△ABC角平分线AE、CF交于点P,BD是△ABC的高,点H在AC上,AF=AH,下列结论:①∠APC=90°+![]() ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
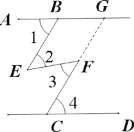
【题目】阅读下列文字,并完成证明;
已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;
证明:如图,延长CF交AB于点G
∵∠2=∠3
∴BE∥CF( )
∴∠1= ( )
又∠1=∠4
∴∠4= ( )
∴AB∥CD( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com