
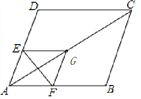
【题目】如图在菱形ABCD中,∠A=60°,AD=![]() ,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
【答案】1或![]()
【解析】分析:首先证明四边形AEGF是菱形,分两种情形:①CG=CB,②GC=GB分别计算即可.
详解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=![]() ,∠DAC=∠BAC=
,∠DAC=∠BAC=![]()
![]() =30°,AC=3,如图,
=30°,AC=3,如图,
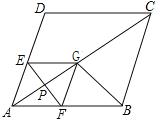
∵EF⊥AG,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EG,AF=FG,
∴AE=EG=GF=FA,
∴四边形AEGF是菱形,
∴AP=PG
①当CB=CG时,∵AG=AC-CG=3-![]() ,
,
∴AP=![]() AG=
AG=![]() .
.
②当GC=GB时,∵∠GCB=∠GBC=∠BAC,
∴△GCB∽△BAC,
∴![]() ,
,
∴GC=1,
∴AG=3-1=2,
∴AP=![]() AG=1.
AG=1.
故答案为1或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)动手操作:
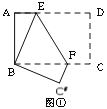
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点![]() 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么![]() 的度数为 。
的度数为 。
(2)观察发现:
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.

(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:无论![]() 为任何实数,抛物线与
为任何实数,抛物线与![]() 轴总有两个交点;
轴总有两个交点;
(2)若A![]() 、B
、B![]() 是抛物线上的两个不同点,求抛物线的表达式和
是抛物线上的两个不同点,求抛物线的表达式和![]() 的值;
的值;
(3)若反比例函数![]() 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为![]() ,且满足2<
,且满足2<![]() <3,求k的取值范围.
<3,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
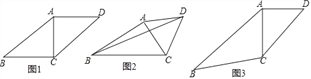
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com