
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
【答案】
(1)解:如图所示:

(2)解:如图,作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA= ![]() ,
,
∴BH=6,
∴OH=8,∴点B的坐标为(8,6),
∵OA=20,OH=8,∴AH=12,
在Rt△AHB中,∵BH=6,
∴AB= ![]() =6
=6 ![]()
∴cos∠BAO= ![]()
(3)解:①当BO=AB时,∵AO=20,∴OH=10,
∴点B沿x轴正半轴方向平移2个单位,
②当AO=AB′时,∵AO=20,∴AB′=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,∴AN= ![]() =2
=2 ![]() .
.
∴点B沿x轴正半轴方向平移(2 ![]() +12)个单位,
+12)个单位,
③当AO=OB″时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴.
∵B的坐标为(8,6),
∴B″P=6,
∴OP= ![]() =2
=2 ![]() ,
,
∴点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位,
﹣8)个单位,
综上所述当点B沿x轴正半轴方向平移2个单位、(2 ![]() +12)个单位,或(2
+12)个单位,或(2 ![]() ﹣8)个单位时,△ABO为等腰三角形
﹣8)个单位时,△ABO为等腰三角形
【解析】(1)作OB,AB的垂直平分线交于一点M,以点M为圆心,MA为半径画圆,则圆M即为所求;(2)如图,作BH⊥OA,垂足为H,在Rt△OHB中,由BO=10,sin∠BOA= ![]() ,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB=
,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB= ![]() =6
=6 ![]() ,求出cos∠BAO=
,求出cos∠BAO= ![]() ;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN=
;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN= ![]() =2
=2 ![]() .求得点B沿x轴正半轴方向平移(2
.求得点B沿x轴正半轴方向平移(2 ![]() +12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP=
+12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP= ![]() =2
=2 ![]() ,点B沿x轴正半轴方向平移(2
,点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位.
﹣8)个单位.


科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位出租车司机某日中午的营运全在市区的环城公路上进行.如果规定:顺时针方向为正,逆时针方向为负,那天中午他拉了五位乘客所行车的里程如下:(单位:千米)+10,﹣7,+4,﹣9,+2.
(1)将最后一名乘客送到目的地时,这位司机距离出车地点的位置如何?
(2)若汽车耗油为![]() 升/千米,那么这天中午这辆出租车的油耗多少升?
升/千米,那么这天中午这辆出租车的油耗多少升?
(3)如果出租车的收费标准是:起步价10元,3千米后每千米2元,问:这个司机这天中午的收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 ![]() m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据: ![]() 1.414,
1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过A(2,-4).
的图象经过A(2,-4).
(1)求k的值.
(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图象.
(4)点B(-2,4),C(-1,5)在这个函数的图象上吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据实际意义可列出夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)根据题意列出t﹣4对应的式子![]() ,与(1)中的式子相减即可.
,与(1)中的式子相减即可.
试题解析:(1)由题意可得,函数关系式为:w=![]() (
(![]() );
);
(2)![]() =
=![]() =
=![]() .(或
.(或![]() ).
).
答:每天多做![]() (或
(或![]() )件夏凉小衫才能完成任务.
)件夏凉小衫才能完成任务.
考点:反比例函数的应用.
【题型】解答题
【结束】
13
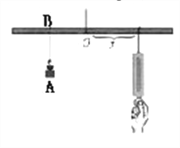
【题目】如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm) | … | 10 | 15 | 20 | 25 | 30 | … |
y(N) | … | 30 | 20 | 15 | 12 | 10 | … |
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会举办权.北京也创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市,张家口也成为本届冬奥会的协办城市.近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,同意新建北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com