
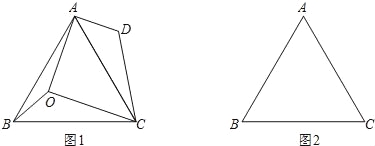
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
【答案】(1)90°;②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,证明见试题解析;
(2)①当α=β=120°时,OA+OB+OC有最小值.证明见试题解析;②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,证明见试题解析。
【解析】
试题分析:(1)①根据周角的定义得到∠AOC=360°﹣120°﹣150°=90°,由于将△BOC绕点C按顺时针方向旋转60°得△ADC,于是得到∠OCD=60°,∠D=∠BOC=120°,根据四边形的内角和即可得到结论;②如图1,连接OD,由于△BOC绕点C按顺时针方向旋转60°得△ADC,得到△ADC≌△BOC,∠OCD=60°,根据全等三角形的性质得到CD=OC,∠ADC=∠BOC=120°,AD=OB,推出△OCD是等边三角形,根据等边三角形的性质得到OC=OD=CD,∠COD=∠CDO=60°,由于∠AOB=150°,∠BOC=120°,得到∠AOC=90°,求得∠AOD=30°,∠ADO=60°,根据勾股定理即可得到结论;
(2)①如图2,由旋转的性质得到O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC..推出△OC O′是等边三角形,根据等边三角形的性质得到OC=O′C=OO′,∠COO′=∠CO′O=60°,由于∠AOB=∠BOC=120°,得到∠AOC=∠A′O′C=120°,推出四点B,O,O′,A′共线,即可得到结论,②根据①的结论即可得到结果.
试题解析:(1)①∠AOB=150°,∠BOC=120°,∴∠AOC=360°﹣120°﹣150°=90°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,∠D=∠BOC=120°,
∴∠DAO=360°﹣∠AOC﹣∠OCD﹣∠D=90°,
故答案为:90°;
②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,
如图1,连接OD,
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△ADC≌△BOC,∠OCD=60°,∴CD=OC,∠ADC=∠BOC=120°,AD=OB,
∴△OCD是等边三角形,∴OC=OD=CD,∠COD=∠CDO=60°,
∵∠AOB=150°,∠BOC=120°,∴∠AOC=90°,
∴∠AOD=30°,∠ADO=60°,∴∠DAO=90°,
在Rt△ADO中,∠DAO=90°,∴OA2+OB2=OD2,∴OA2+OB2=OC2;
(2)①当α=β=120°时,OA+OB+OC有最小值.
如图2,将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′,
∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°,
∴O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC.
∴△OC O′是等边三角形,∴OC=O′C=OO′,∠COO′=∠CO′O=60°,
∵∠AOB=∠BOC=120°,∴∠AOC=∠A′O′C=120°,
∴∠BOO′=∠OO′A′=180°,∴四点B,O,O′,A′共线,
∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小;
②∵∠AOB=∠BOC=120°,∴∠AOC=120°,∴O为△ABC的中心,
∵四点B,O,O′,A′共线,∴BD⊥AC,∵将△AOC绕点C按顺时针方向旋转60°得△A′O′C,
∴A′C=AC=BC,∴A′B=2BD,在Rt△BCD中,BD=![]() BC=
BC=![]() ,∴A′B=
,∴A′B=![]() ,
,
∴当等边△ABC的边长为1时,OA+OB+OC的最小值A′B=![]() .
.



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
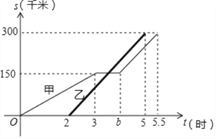
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a和b的值.
(2)求两车在途中相遇时t的值.
(3)当两车相距60千米时,t= 时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种型号计算器,A型号计算器的进货价格为每台30元,B型号计算器的进货价格为每台40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)分别求商场销售A、B两种型号计算器每台的销售价格.
(2)商场准备用不多于2 500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?【利润=销售价格-进货价格】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③a<-1;④b2+8a>4ac,其中正确的有( )
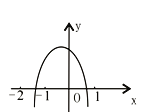
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com