
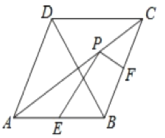
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点E,F分别是边
,点E,F分别是边![]() ,
,![]() 的中点,
的中点,![]() 是
是![]() 上的动点,那么
上的动点,那么![]() 的最小值是_______.
的最小值是_______.
【答案】5
【解析】
设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,根据菱形的性质推出N是AD中点,P与O重合,推出PE+PF=NF=AB,根据勾股定理求出AB的长即可.
设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,
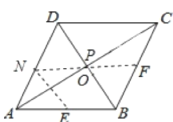
∴PN=PE,
∵四边形ABCD是菱形,
∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,
∵E为AB的中点,
∴N在AD上,且N为AD的中点,
∵AD∥CB,
∴∠ANP=∠CFP,∠NAP=∠FCP,
∵AD=BC,N为AD中点,F为BC中点,
在△ANP和△CFP中
∵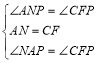 ,
,
∴△ANP≌△CFP(ASA),
∴AP=CP,
即P为AC中点,
∵O为AC中点,
∴P、O重合,
即NF过O点,
∵AN∥BF,AN=BF,
∴四边形ANFB是平行四边形,
∴NF=AB,
∵菱形ABCD,
∴AC⊥BD,OA=![]() AC=4,BO=
AC=4,BO=![]() BD=3,
BD=3,
由勾股定理得:AB=![]() =5,
=5,
故答案为:5.


科目:初中数学 来源: 题型:
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数.

请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB__________
所以∠DCE=∠B__________
又因为∠B=95°,
所以∠DCE=________°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB=________=________°,
因为DC∥AB
所以∠DCA=∠CAB,__________
所以∠DCA=________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
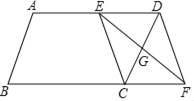
【题目】如图,平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
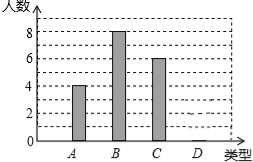
【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 过点
过点![]() ,
,![]() .
.
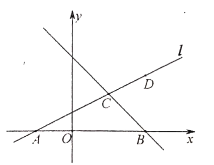
(1)求直线![]() 的解析式;
的解析式;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .
.
①求![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的2倍,如果存在,求出点
面积的2倍,如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为P0,P1,P2,P3,则P0,P1,P2,P3中最大的是( )
A. P0 B. P1 C. P2 D. P3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
对于任意一个三位数正整数n,如果n的各个数位上的数字互不相同,且都不为零,那么称这个数为“陌生数”,将一个“陌生数”的三个数位上的数字交换顺序,可以得到5个不同的新“陌生数”,把这6个陌生数的和与111的商记为M(n).例如n=123,可以得到132.213.231.312.321这5个新的“陌生数”,这6个“陌生数”的和为123+132+213+231+312+321=1332,因为![]() ,所以M(123)=12.
,所以M(123)=12.
(1)计算:M(125)和M(361)的值;
(2)设s和t都是“陌生数”,其中4和2分别是s的十位和个位上的数字,2和5分别是t的百位和个位上的数字,且t的十位上的数字比s的百位上的数字小2;规定:![]() .若
.若![]() ,则k的值是多少?
,则k的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4
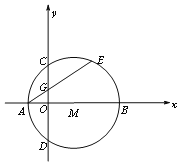
(1)求点C的坐标;
(2)连接MG、BC,求证:MG∥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com