
【题目】在有理数的范围内,我们定义三个数之间的新运算法则“⊕”:![]() ⊕
⊕![]() ⊕
⊕![]() =
=![]() .如:
.如:![]() ⊕2⊕3=
⊕2⊕3=![]() .
.
①根据题意,3⊕![]() ⊕
⊕![]() 的值为__________;
的值为__________;
②在![]() 这15个数中,任意取三个数作为
这15个数中,任意取三个数作为![]() ,
,![]() ,
,![]() 的值,进行“
的值,进行“![]() ⊕
⊕![]() ⊕
⊕![]() ”运算,在所有计算结果中的最大值为__________;最小值为__________.
”运算,在所有计算结果中的最大值为__________;最小值为__________.
 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
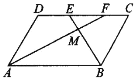
【题目】如图所示,已知四边形ABCD是平行四边形,∠C=70°,若AF、BE分别为∠DAB、∠CBA的平分线.
求证:(1)DF=EC;(2)求∠DFA的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
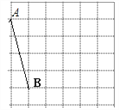
【题目】如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;
(2)在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边上一点,将△ABD绕点A逆时针旋转60°得到△ACE,连接DE,则下列说法不一定正确的是( )
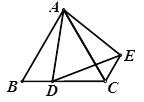
A. △ADE是等边三角形 B. AB∥CE C. ∠BAD=∠DEC D. AC=CD+CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象
的图象![]() 分别与x轴,y轴交于A、B两点,正比例函数的图象
分别与x轴,y轴交于A、B两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.

(1)求m的值及![]() 的解析式;
的解析式;
(2)求得![]() 的值为______;
的值为______;
(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 可以围成三角形,直接写出k的取值范围.
可以围成三角形,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取四张,根据牌面上的数字进行混合运算(每一张牌必须用一次且只能用一次,可以加括号),使得运算结果为24或﹣24,其中红色扑克牌代表负数,黑色扑克牌代表正数.J.Q.K.A分别代表11.12.13.1,小明抽到了黑桃7,黑桃3,梅花3,梅花7,他运用下面的方法凑成了:![]() .
.
(1)如果抽到的是黑桃7,黑桃5,红桃5,梅花7,你能凑成24吗?
(2)如果抽到的是黑桃A,方块2,黑桃2,黑桃3,你能凑成24吗?(请用两种方法)
(3)如果抽到的是黑桃Q,红桃Q,梅花3,方块A,你能凑成24吗?(请用多种方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
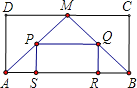
【题目】如图,在矩形ABCD中,M为CD的中点,连接AM、BM,分别取AM、BM的中点P、Q,以P、Q为顶点作第二个矩形PSRQ,使S、R在AB上![]() 在矩形PSRQ中,重复以上的步骤继续画图
在矩形PSRQ中,重复以上的步骤继续画图![]() 若
若![]() ,矩形ABCD的周长为
,矩形ABCD的周长为![]() 则:
则:![]() ______;
______;![]() 第n个矩形的边长分别是______.
第n个矩形的边长分别是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区的数学爱好者申请了一项省级课题——《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如下两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
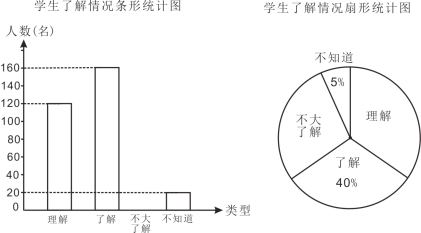
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
①S1+S2=S3+S4② S2+S4= S1+ S3
③若S3=2S1,则S4=2S2④若S1= S2,则P点在矩形的对角线上
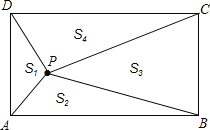
其中正确的结论的序号是 ▲ (把所有正确结论的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com