
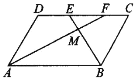
【题目】如图所示,已知四边形ABCD是平行四边形,∠C=70°,若AF、BE分别为∠DAB、∠CBA的平分线.
求证:(1)DF=EC;(2)求∠DFA的大小。
【答案】(1)见解析;(2)35°.
【解析】
(1)由角平分线的定义得出∠DAF=∠BAF,再由AB∥CD,得∠DFA=∠BAF,从而得出∠DAF=∠DFA,即AD=DF,同理得出BC=EC,由平行四边形的性质得出DF=EC;
(2)先根据平行四边形的性质得出∠DAB=70°,AB∥DC,利用平行线的性质得出∠FAB=∠DFA,再由角平分线得出∠DFA=∠FAB=![]() ∠DAB=35°.
∠DAB=35°.
证明:(1)∵AF、BE分别为∠DAB、∠CBA的平分线,
∴∠DAF=∠BAF,
又在四边形ABCD中DC∥AB,
∴∠DFA=∠BAF,
从而,∠DAF=∠DFA
∴AD=DF,同理BC=EC。
又AD=BC
∴DF=EC
(2)∵四边形ABCD是平行四边形, ∠C=70°, ∴∠DAB=70°,AB∥DC, ∴∠FAB=∠DFA, ∵AF平分∠DAB,∴∠FAB=![]() ∠DAB=35°, ∴∠DFA=∠DAF=35°.
∠DAB=35°, ∴∠DFA=∠DAF=35°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】旅客乘车按规定可随身携带一定重量的行李,如果超过规定,那么需购买行李票,设行李费![]() (元)是行李重量
(元)是行李重量![]() 的函数,其图像如图所示.
的函数,其图像如图所示.
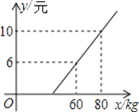
(1)求y与x之间的函数关系式;
(2)旅客最多可免费携带行李的重量;
(3)某旅客所买的行李票的费用为415元,求他所带行李的质量范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一刻度尺放在数轴上.

①若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 5,则 1cm 对应数轴上的点表示的数是 2;
②若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 9,则 1cm 对应数轴上的点表示的数是 3;
③若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为-2 和 2,则 1cm 对应数轴上的点表示的数是-1;
④若刻度尺上 0cm 和 4 cm 对应数轴上的点表示的数分别为-1 和 1,则 1cm 对应数轴上的点表示的数是-0.5. 上述结论中,所有正确结论的序号是 ( )
A.①②B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,完成下列题目:
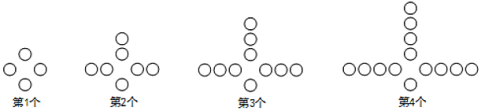
(1)填写下表:
图案序号 | 1 | 2 | 3 | 4 | … |
|
○个数 | 4 | 7 | … |
(2)若按上面的规律继续摆放,是否存在第![]() 个图形,其中恰好含有2020个○?
个图形,其中恰好含有2020个○?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店试销一种成本为10元的文具.经试销发现,每天销售件数y(件)是每件销售价格x (元)的一次函数,且当每件按15元的价格销售时,每天能卖出50件;当每件按20元的价格销售时,每天能卖出40件.
(1)试求y关于x的函数解析式(不用写出定义域);
(2)如果每天要通过销售该种文具获得450元的利润,那么该种文具每件的销售价格应该定为多少元?(不考虑其他因素)
查看答案和解析>>
科目:初中数学 来源: 题型:
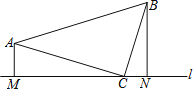
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数的范围内,我们定义三个数之间的新运算法则“⊕”:![]() ⊕
⊕![]() ⊕
⊕![]() =
=![]() .如:
.如:![]() ⊕2⊕3=
⊕2⊕3=![]() .
.
①根据题意,3⊕![]() ⊕
⊕![]() 的值为__________;
的值为__________;
②在![]() 这15个数中,任意取三个数作为
这15个数中,任意取三个数作为![]() ,
,![]() ,
,![]() 的值,进行“
的值,进行“![]() ⊕
⊕![]() ⊕
⊕![]() ”运算,在所有计算结果中的最大值为__________;最小值为__________.
”运算,在所有计算结果中的最大值为__________;最小值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com