
【题目】旅客乘车按规定可随身携带一定重量的行李,如果超过规定,那么需购买行李票,设行李费![]() (元)是行李重量
(元)是行李重量![]() 的函数,其图像如图所示.
的函数,其图像如图所示.
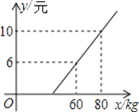
(1)求y与x之间的函数关系式;
(2)旅客最多可免费携带行李的重量;
(3)某旅客所买的行李票的费用为415元,求他所带行李的质量范围.
科目:初中数学 来源: 题型:
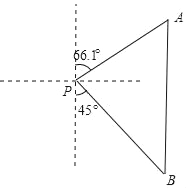
【题目】如图,一艘海轮位于灯塔P的北偏东66.1°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
参考数据:sin66.1°≈0.91,cos66.1°≈0.41,tan64°≈2.26,![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
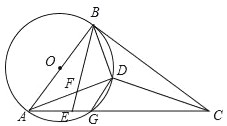
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°,∠B'=110°,∠BCA'的度数是( )
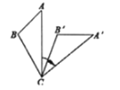
A.110°B.80°C.40°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过![]() 轴正半轴上的任意一点
轴正半轴上的任意一点![]() ,作
,作![]() 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于点
的图象交于点![]() 和点
和点![]() ,点
,点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
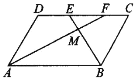
【题目】如图所示,已知四边形ABCD是平行四边形,∠C=70°,若AF、BE分别为∠DAB、∠CBA的平分线.
求证:(1)DF=EC;(2)求∠DFA的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com