
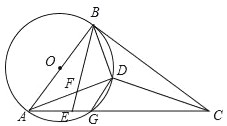
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
【答案】(1)证明见解析;(2)证明见解析;(3)正确的结论:AD﹣BD的值不变,证明见解析,AD﹣BD=![]() .
.
【解析】试题分析:(1)根据三角形内心的性质得出∠DBC=∠DBE,进而根据已知求得∠DBC=∠BAD,根据圆周角定理即可证得![]() 从而求得AB⊥BC,证得结论;
从而求得AB⊥BC,证得结论;
(2)连接![]() ,根据圆内接四边形外角的性质得出
,根据圆内接四边形外角的性质得出![]() 由三角形外角的性质求得
由三角形外角的性质求得![]() 证得
证得![]() 进而求得
进而求得![]() 由三角形内心的性质得出
由三角形内心的性质得出![]() 然后根据AAS证得△DEF≌△DEG,从而证得
然后根据AAS证得△DEF≌△DEG,从而证得![]()
(3)在AD上截取DH=BD,连接BH、BG,证得![]() 是等腰直角三角形,得出
是等腰直角三角形,得出![]() 然后证得△ABH∽△GBD,得出
然后证得△ABH∽△GBD,得出![]() 求得
求得![]() 即可求得
即可求得![]()
试题解析:(1)证明:∵D为△BCE内心,
∴∠DBC=∠DBE,
∵∠DBE=∠BAD.
∴∠DBC=∠BAD,
∵AB是![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
即![]()
∴AB⊥BC,
∴BC是![]() 的切线;
的切线;
(2)证明:如图1,连接DE,
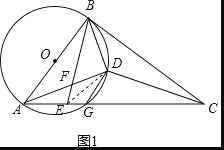
∵∠DBC=∠BAD,∠DBC=∠DBE,
∴∠DBE=∠BAD,
∴∠ABF+∠BAD=∠ABF+∠DBE,
∴∠BFD=∠ABD,
∵∠DGC=∠ABD,
∴∠BFD=∠DGC,
∴∠DFE=∠DGE,
∵D为△BCE内心,
∴∠DEG=∠DEB,
在△DEF和△DEG中
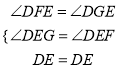 ,
,
∴△DEF≌△DEG(AAS),
∴DF=DG;
(3)ADBD的值不变;
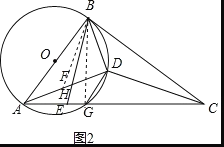
如图2,在AD上截取DH=BD,连接BH、BG,
∵AB是直径,
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴∠AHB=∠BDG,
∵∠BAD=∠BGD,
∴△ABH∽△GBD,
∴![]()
∵DG=1,
∴![]()
∵ADBD=ADDH=AH,
∴![]()


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
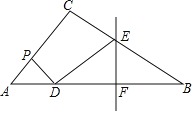
【题目】如图,在△ABC中,∠C=![]() ,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
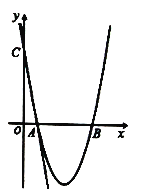
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求抛物线解析式及![]() 点坐标;
点坐标;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上一动点,连接
为抛物线上一动点,连接![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求此时点
倍,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有两点A、B,点B在点A的右侧,且AB=10,点A表示的数为﹣6.动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动.
(1)写出数轴上点B表示的数;
(2)经过多少时间,线段AP和BP的长度之和为18?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上![]() 四个点.
四个点.
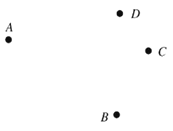
(1)按下列要求画图(不写画法)
①连接![]() ,
,![]() ;②作直线
;②作直线![]() ;③作射线
;③作射线![]() ,交
,交![]() 于点
于点![]() .
.
(2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段![]() ,
,![]() ,
,![]() ,可知
,可知![]() __________
__________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某河流防污治理工程已正式启动,由甲队单独做5个月后,乙队再加入合作3个月就可以完成这项工程。已知若甲队单独做需要10个月可以完成。
(1)乙队单独完成这项工程需要几个月?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
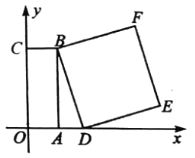
【题目】如图,以矩形![]() 的顶点
的顶点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,![]() ,
,![]() ,点
,点![]() 为
为![]() 轴上一动点,以
轴上一动点,以![]() 为一边在
为一边在![]() 右侧作正方形
右侧作正方形![]() .
.
(1)若点![]() 与点
与点![]() 重合,请直接写出点
重合,请直接写出点![]() 的坐标.
的坐标.
(2)若点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x-1成正比例,且函数图象经过点(3,-6).
(1)求这个函数的解析式并画出这个函数图象.
(2)已知图象上的两点C(x1,y1)、D(x2,y2),如果x1>x2,比较y1、y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com