
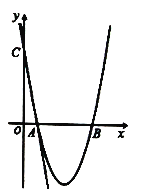
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求抛物线解析式及![]() 点坐标;
点坐标;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上一动点,连接
为抛物线上一动点,连接![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求此时点
倍,求此时点![]() 的坐标.
的坐标.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值: x﹣2(x﹣![]() y2)+(﹣2x+
y2)+(﹣2x+![]() y2),其中x=2,y=﹣3
y2),其中x=2,y=﹣3
(2)已知:若a,b互为相反数,c,d互为倒数,m的绝对值为最小正整数,求代数式﹣2cd+![]() ﹣m的值
﹣m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图.根据统计图,下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中,正确的是( )


A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大
C. 张亮的百分比与李娜的百分比一样大 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
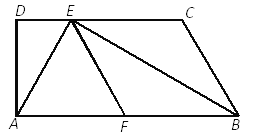
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
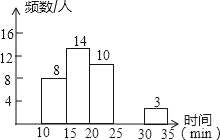
【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
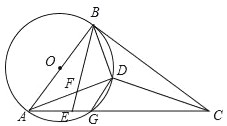
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-7平移后的图象l经过点(-3,-2),
(1)求l的函数解析式;并画出该函数的图象;
(2)l与x轴交于点A,点P是l上一点,且S△AOP=![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com