
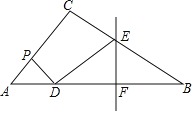
【题目】如图,在△ABC中,∠C=![]() ,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.若AC=6,BC=8,PA=2,则线段DE的长为________
【答案】![]()
【解析】
连接OD,根据等腰三角形的性质得到∠A=∠PDA,根据线段垂直平分线的性质得到EB=ED,于是得到DE⊥DP;连接PE,设DE=x,则EB=ED=x,CE=8x,根据勾股定理即可得到结论.
∵PD=PA,
∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°90°=90°,
∴DE⊥DP,
连接PE,
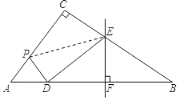
设DE=x,则EB=ED=x,CE=8x,
∵∠C=∠PDE=90°,
∴PC2+CE2=PE2=PD2+DE2,
∴42+(8x)2=22+x2,
解得:x=![]() ,
,
则DE=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,且线段AB=4,CD=6,已知A表示的数是﹣10,C表示的数是8,若线段AB以每秒6个单位长度的速度,线段CD以每秒2个单位长度的速度在数轴上运动(A在B左侧,C在D左侧)
(1)B,D两点所表示的数分别是 、 ;
(2)若线段AB向右运动,同时线段CD向左运动,经过多少秒时,BC=2;
(3)若线段AB、CD同时向右运动,同时点P从原点出发以每秒1个单位长度的速度向右运动,经过多少秒时,点P到点A,C的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值: x﹣2(x﹣![]() y2)+(﹣2x+
y2)+(﹣2x+![]() y2),其中x=2,y=﹣3
y2),其中x=2,y=﹣3
(2)已知:若a,b互为相反数,c,d互为倒数,m的绝对值为最小正整数,求代数式﹣2cd+![]() ﹣m的值
﹣m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第n个数记为an.
(1)请写出29后面的第一个数;
(2)通过计算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根据你发现的规律求a100的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
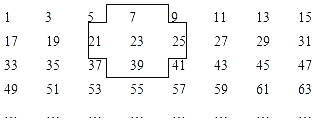
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,D是BC边上一点,∠ADC=3∠BAD,BD=8,DC=7,则AB的值为( )
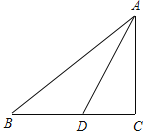
A. 15 B. 20 C. 2![]() +7 D. 2
+7 D. 2![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图.根据统计图,下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中,正确的是( )


A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大
C. 张亮的百分比与李娜的百分比一样大 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
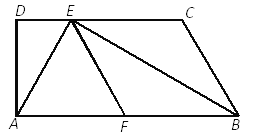
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
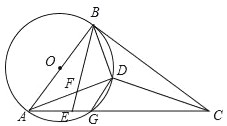
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com