
【题目】(1)解不等式组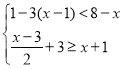
(2)先化简分式![]() ,然后在0,1,2,3中选一个你认为合适的a值,代入求值。
,然后在0,1,2,3中选一个你认为合适的a值,代入求值。
【答案】(1)﹣2<x≤1(2)见解析
【解析】
(1)通过计算得出不等式组中1-3(x-1)<8-x的解集为x>﹣2,![]() —+3≥x+1的解集为x≤1,得出不等式组的解集为﹣2<x≤1.
—+3≥x+1的解集为x≤1,得出不等式组的解集为﹣2<x≤1.
(2)先化简得出结果,要想式分式有意义,则分式的分母不能为0,即x≠0、1、3.则x只能取0,1,2,3中的2,将2带入结果中即可得出最终结果.
(1) 由1-3(x-1)<8-x得:
1-3x+3<8-x,
1+3-8<-x+3x,
﹣4<2x,
则x>﹣2.
由![]() +3≥x+1得:
+3≥x+1得:
x-3+6≥2x+2
﹣3+6-2≥2x-x
则x≤1
所以不等式组的解集为﹣2<x≤1.
(2)![]() ÷
÷![]() -
- ![]()
=![]() ×
×![]() -
- ![]()
=![]() ×
×![]() -
- ![]()
=![]() +
+![]()
=![]() +
+![]()
=2![]()
要想使分式有意义,必须使分式的分母不能为0,
除法中除数不能为0,
即![]() +3≠0、
+3≠0、![]() (
(![]() )≠0、a-3≠0、a-1≠0
)≠0、a-3≠0、a-1≠0
故a≠0、-3、1、3.
所以a只能取0、1、2、3中的2,
将2代入化简结果2a得:
2a=2×2,
=4.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,D是BC边上一点,∠ADC=3∠BAD,BD=8,DC=7,则AB的值为( )
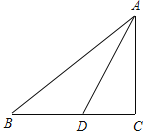
A. 15 B. 20 C. 2![]() +7 D. 2
+7 D. 2![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
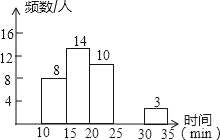
【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
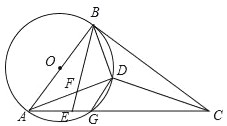
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG。求证:①∠BEA =∠G,② EF=FG。
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售, 每吨利润为7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨, 如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案1:将蔬菜全部进行粗加工;
方案2:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案3:将一部分蔬菜进行精加工, 其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案? 请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少,最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com