
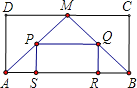
【题目】如图,在矩形ABCD中,M为CD的中点,连接AM、BM,分别取AM、BM的中点P、Q,以P、Q为顶点作第二个矩形PSRQ,使S、R在AB上![]() 在矩形PSRQ中,重复以上的步骤继续画图
在矩形PSRQ中,重复以上的步骤继续画图![]() 若
若![]() ,矩形ABCD的周长为
,矩形ABCD的周长为![]() 则:
则:![]() ______;
______;![]() 第n个矩形的边长分别是______.
第n个矩形的边长分别是______.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】某商店试销一种成本为10元的文具.经试销发现,每天销售件数y(件)是每件销售价格x (元)的一次函数,且当每件按15元的价格销售时,每天能卖出50件;当每件按20元的价格销售时,每天能卖出40件.
(1)试求y关于x的函数解析式(不用写出定义域);
(2)如果每天要通过销售该种文具获得450元的利润,那么该种文具每件的销售价格应该定为多少元?(不考虑其他因素)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数的范围内,我们定义三个数之间的新运算法则“⊕”:![]() ⊕
⊕![]() ⊕
⊕![]() =
=![]() .如:
.如:![]() ⊕2⊕3=
⊕2⊕3=![]() .
.
①根据题意,3⊕![]() ⊕
⊕![]() 的值为__________;
的值为__________;
②在![]() 这15个数中,任意取三个数作为
这15个数中,任意取三个数作为![]() ,
,![]() ,
,![]() 的值,进行“
的值,进行“![]() ⊕
⊕![]() ⊕
⊕![]() ”运算,在所有计算结果中的最大值为__________;最小值为__________.
”运算,在所有计算结果中的最大值为__________;最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
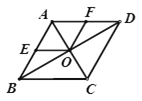
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E、F分别是AB、AD的中点.
(1)若AC=10,BD=24,求菱形ABCD的周长;
(2)连接OE、OF,若AB⊥BC,则四边形AEOF是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中小学生每天在校体育活动时间不低于1小时”![]() 为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生
为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生![]() 根据调查结果绘制成的统计图
根据调查结果绘制成的统计图![]() 部分
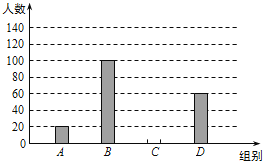
部分![]() 如图所示,其中分组情况是:
如图所示,其中分组情况是:
A组:![]() B组:
B组:![]() C组:
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
![]() 组的人数是______.
组的人数是______.
![]() 本次调查数据的中位数落在______组内;
本次调查数据的中位数落在______组内;
![]() 若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
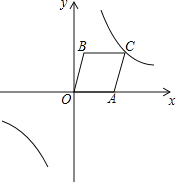
【题目】如图,![]() ,以OA、OB为边作平行四边形OACB,反比例函数
,以OA、OB为边作平行四边形OACB,反比例函数![]() 的图象经过点C.
的图象经过点C.
![]() 求k的值;
求k的值;
![]() 根据图象,直接写出
根据图象,直接写出![]() 时自变量x的取值范围;
时自变量x的取值范围;
![]() 将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
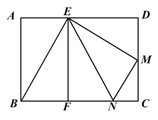
【题目】如图,在矩形ABCD中,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,若点M恰好是边CD的中点,那么![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com