
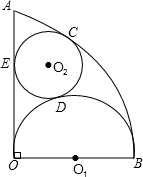
 如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.
如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径. 分析 连接OC、O1 O2、O2 E,作O2 M⊥OB于M,由相切两圆的性质得OC经过点O2,O1 O2经过点D,设⊙O2的半径为x,则OM=EO2=x,O1 M=2-x,OO2=4-x,O1 O2=x+2,由勾股定理得出方程,解方程即可求得.
解答 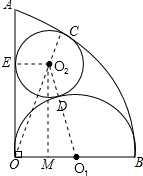 解:连接OC、O1 O2、O2 E,作O2 M⊥OB于M,如图所示:
解:连接OC、O1 O2、O2 E,作O2 M⊥OB于M,如图所示:
则OC经过点O2,O1 O2经过点D,∠O2 MO=∠O2 MO1=90°,
设⊙O2的半径为x,
则OM=EO2=x,O1 M=2-x,OO2=4-x,O1 O2=x+2,
由勾股定理得:O2 M2=OO2 2-OM2=O1 O2 2-O1 M2,
即(4-x)2-x2=(x+2)2-(2-x)2,
解得:x=1,
即⊙O2的半径为1.
点评 本题考查了相切两圆的性质、勾股定理;熟练掌握相切两圆的性质,运用勾股定理得出方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
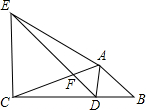 如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.
如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
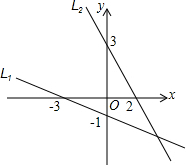 如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
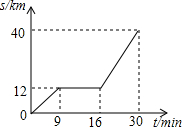 如图是某汽车行驶的路程s(km)与时间t(m/n)的函数关系图,观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程s(km)与时间t(m/n)的函数关系图,观察图中所提供的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com