
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() 轴,且
轴,且![]() .
.
(1)求点![]() ,
,![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)点![]() 为
为![]() 轴右侧抛物线上一点.
轴右侧抛物线上一点.
①如图①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
②如图②,抛物线上一点![]() 的横坐标为2,直线
的横坐标为2,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)令y=0,解方程即可求出点A、B的坐标,由此可求得AB的长及对称轴,再根据![]() 即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
(2)①作![]() 于
于![]() ,根据
,根据![]() 平分
平分![]() 可得
可得![]() ,进而设
,进而设![]() ,根据
,根据![]() 可得方程
可得方程![]() 求解即可求得点E坐标为
求解即可求得点E坐标为![]() ,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
②分两种情形(Ⅰ)若点![]() 在
在![]() 点上方,如图②,(Ⅱ)若点
点上方,如图②,(Ⅱ)若点![]() 在点
在点![]() 下方,如图③,分别列出方程即可解决.
下方,如图③,分别列出方程即可解决.
解:(1)令![]() ,则
,则![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]()
∴![]() ,
,
∵点C在y轴上且![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①作![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
设![]() 对应函数表达式为
对应函数表达式为![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
∴![]() 对应函数表达式为
对应函数表达式为![]() .
.
∵![]() ,
,
∴二次函数表达式为![]() ,
,
∴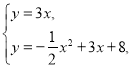 ,
,
解得![]() 或
或![]() (舍去)
(舍去)
∴点![]() .
.
②∵当![]() 时,
时,![]() ,∴点
,∴点![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]()
把点![]() 、点
、点![]() 代入,
代入,
得![]()
解得![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∴点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅰ)若点![]() 在
在![]() 点上方,如图②.
点上方,如图②.
过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .
.
∵![]() ,
,
∴![]() 轴,
轴,
∵![]() 轴,
轴,
∴点![]() 与点
与点![]() 重合,
重合,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
把![]() 代入
代入![]()
得,![]() .
.
∴![]() .
.
(Ⅱ)若点![]() 在点
在点![]() 下方,如图③.
下方,如图③.
过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() .
.
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]()
∵![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() ,得
,得
![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
代入![]() 得
得
![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
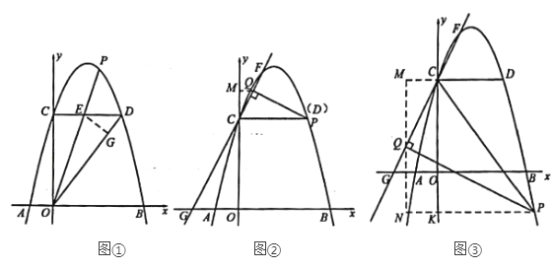
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
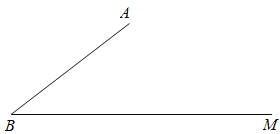
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.点D为BC中点,E为边AB上一动点(不与A、B点重合),以点D为直角顶点、以射线DE为一边作∠MDN=90°,另一条边DN与边AC交于点F.下列结论中正确结论是( )
①BE=AF;
②△DEF是等腰直角三角形;
③无论点E、F的位置如何,总有EF=DF+CF成立;
④四边形AEDF的面积随着点E、F的位置不同发生变化.
A.①③B.②③C.①②D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
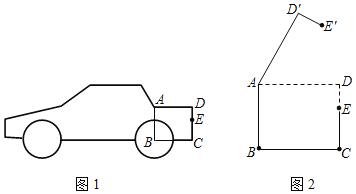
【题目】图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=96厘米,DE=28厘米,EC=42厘米.
(1)求点D′到BC的距离;
(2)求E、E′两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,对“垃圾分类”的知晓情况分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.其中,
四类.其中,![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
“垃圾分类”知晓情况各类别人数条形统计图 “垃圾分类”知晓情况各类别人数扇形统计图

根据以上信息解决下列问题:
(1)初三(1)班参加这次调查的学生有______人,扇形统计图中类别![]() 所对应扇形的圆心角度数为______°;
所对应扇形的圆心角度数为______°;
(2)求出类别![]() 的学生数,并补全条形统计图;
的学生数,并补全条形统计图;
(3)类别![]() 的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
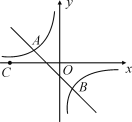
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出,当kx+b<![]() 时,x的取值范围;
时,x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: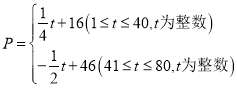 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
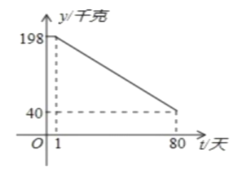
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com