
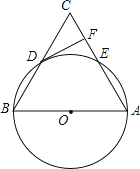
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,![]() 求
求![]() 长(结果保留π).
长(结果保留π).
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;
(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
试题解析:(1)证明:连接OD,如图所示.
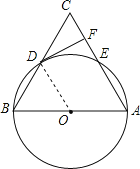
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°-∠CDF-∠ODF=60°
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴BD弧的长= ![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在小方格纸上按下面的方式涂色:

① ② ③ ④
(1)填表:
图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
涂色的小方格数 |
(2)像这样,第 n 个图形要涂色的小方格数是__________,第100个图形要涂色的小方格数是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点.
如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
如图3,点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
如图4,点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示-2和-5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是_______;
(2)数轴上表示x和-1的两点A和B之间的距离是___________,如果∣AB∣=2,那么x为____________;
(3)当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
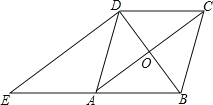
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com