练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
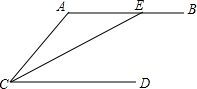
    4．如图，已知∠ACE=∠AEC，CE平分∠ACD，则AB∥CD，用推理的方法说明它是一个真命题．

    分析 根据角平分线的定义和平行线的判定解答即可．

    解答 解：∵CE平分∠ACD，
    ∴∠ACE=∠ECD，
    ∵∠ACE=∠AEC，
    ∴∠ECD=∠AEC，
    ∴AB∥CD．

    点评 此题考查平行线的判定，关键是根据角平分线的定义得出∠ACE=∠ECD．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

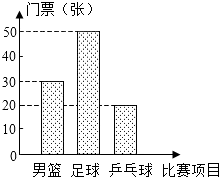    14．下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格，某公司购买的门票种类、数量绘制的条形统计图如图．
    比赛项目票价（元/张）
    男  篮1000
    足  球800
    乒乓球x
    依据上列图、表，回答下列问题：
    （1）其中观看男篮比赛的门票有30 张；观看乒乓球比赛的门票占全部门票的20%；
    （2）公司决定采用随机抽取的方式把门票分配给100名员工，在看不到门票的条件下，每人抽取一张（假设所有的门票形状、大小、质地等完全相同且充分洗匀），问员工小亮抽到足球门票的概率是$\frac{1}{2}$；
    （3）若购买乒乓球门票的总款数占全部门票总款数的$\frac{1}{8}$，试求每张乒乓球门票的价格．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程：（2y+1）2+4（2y+1）+4=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：$\sqrt{7+4\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．设关于x的一元二次方程x2+kx-1=0的两实根分别x1，x2，且满足x1+x2=x2•x2，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．方程2x2-3x+1=0化为（x+a）2=b（a，b为常数）的形式，正确的是（　　）
    A．（x-$\frac{3}{2}$）2=16B．（2x-$\frac{3}{4}$）2=$\frac{1}{16}$C．（x-$\frac{3}{4}$）2=$\frac{1}{16}$D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知四个不等实数a，b，c，d任意三个实数和为2、4、5、7，则abcd=-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．△ABC的三个外角度数之比是2：3：4，则三个内角度数之比是（　　）
    A．4：3：2B．3：2：4C．5：3：1D．3：1：5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

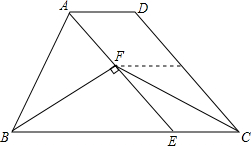    11．如图，在梯形ABCD中，AD∥BC，AB=CD，AE∥DC交BC于点E，BF⊥AE于F，AD=2，BC=7，CF=4，且∠ABF=∠DCF．
    （1）求AB的长；
    （2）求梯形ABCD的面积．

    查看答案和解析>>

    同步练习册答案