解:(1)运动t秒后OC=t,则可得点D的坐标为(2+t,0),

,
解得:

,即点A的坐标为(4,2),
∵点E是OA的中点,
∴点E的坐标为(2,1).
(2)①当∠EDC=90°时,此时点E坐标为:(2,1),点D坐标为(2,0),
则2+t=2,
解得:t=0;
②当∠ECD=90°时,此时点E坐标为:(2,1),点C坐标为(2,0),
则t=OC=2;
③当∠CED=90°时,过点E作EP⊥x轴于点P,

∵点E坐标为(2,1),
∴CP=2-t,PD=2+t-2=t,EP=1,
由CE
2+ED
2=CD
2,可得(2-t)
2+1
2+t
2+1
2=2
2,
解得:t=1,
综上可得当t=0或t=1或t=2时,△DEC是直角三角形.
(3)如图,作CE关于x轴的对称线段,CE',将CE'向右平移至FE'',当FE''与AF共线时四边形AECF的周长最小,

∵C(t,0),CD=2,点F是CD的中点,
∴CF=1,点F(t+1,0),
设过A(4,2),E''(3,-1)两点的直线表达式为y=kx+b,
则

,
解得:

,
则直线AE''的表达式为:y=3x-10,
当点F(t+1,0)在直线AE''上时,3(t+1)-10=0,
解得:t=

,
则存在t=

,使得四边形AECF的周长最小.
分析:(1)用t表示出OC的长度,然后可得出点D的坐标,联立两直线解析式可得出点A的坐标,根据点E是OA的中点,可得出点E的坐标;
(2)分三种情况讨论即可,①∠EDC=90°,②∠ECD=90°,③∠CED=90°,分别求出t的值.
(3)作CE关于x轴的对称线段,CE',将CE'向右平移至FE'',当FE''与AF共线时四边形AECF的周长最小,确定AE''的直线解析式,将点F的坐标代入可求出t的值.
点评:本题考查了一次函数综合题,涉及了动点问题、直角三角形及待定系数法求函数解析式及三点共线的知识,综合性较强,解答第三问要注意两点之间线段最短的运用,要求同学们能将所学的知识融会贯通.

 交于点A,点E为线段OA的中点,长为2个单位的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动的时间为t秒(t≥0).
交于点A,点E为线段OA的中点,长为2个单位的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动的时间为t秒(t≥0).
 ,
, ,即点A的坐标为(4,2),
,即点A的坐标为(4,2),

 ,
, ,
, ,
, ,使得四边形AECF的周长最小.
,使得四边形AECF的周长最小.

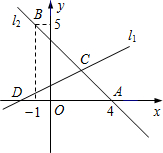 l2交于点C.
l2交于点C. 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.