练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，在平面直角坐标系xOy中，等边△AOB的边长为6，点C在边OA上，点D在边AB上，且OC=3BD，反比例函数（k≠0）的图象恰好经过点C和点D，则k的值为（　　）

    A. B. C. D.

    【答案】A

    【解析】

    试题过点C作CE⊥x轴于点E，过点D作DF⊥x轴于点F，如图所示．

    设BD=a，则OC=3a．

    ∵△AOB为边长为6的等边三角形，∴∠COE=∠DBF=60°，OB=6．

    在Rt△COE中，∠COE=60°，∠CEO=90°，OC=3a，∴∠OCE=30°，∴OE=a，CE= = a，∴点C（a， a）．

    同理，可求出点D的坐标为（6﹣a，a）．

    ∵反比例函数（k≠0）的图象恰好经过点C和点D，∴k=a×a=（6﹣a）×a，∴a=，k=．故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB＝90°，将△ABC沿着一条直线折叠后，使点A与点C重合（如图②）

    （1）在图①中画出折痕所在的直线l，问直线l是线段AC的　 　线；

    （2）设直线l与AB、AC分别相交于点M、N，连结CM，若△CMB的周长是21cm，AB＝14cm，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

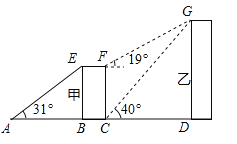
    【题目】某学校教学楼（甲楼）的顶部E和大门A之间挂了一些彩旗．小颖测得大门A距甲楼的距离AB是31cm，在A处测得甲楼顶部E处的仰角是31°．

    （1）求甲楼的高度及彩旗的长度；（精确到0.01m）

    （2）若小颖在甲楼楼底C处测得学校后面医院楼（乙楼）楼顶G处的仰角为40°，爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°，求乙楼的高度及甲乙两楼之间的距离．（精确到0.01m）

    （cos31°≈0.86，tan31°≈0.60，cos19°≈0.95，tan19°≈0.34，cos40°≈0.77，tan40°≈0.84）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

    （1）在这次调查中，喜欢篮球项目的同学有　 　人，在扇形统计图中，“乒乓球”的百分比为　 　%，如果学校有800名学生，估计全校学生中有　 　人喜欢篮球项目．

    （2）请将条形统计图补充完整．

    （3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠B=90°，AB=3cm，BC=4cm.

    （1）如图1，点P从点A出发，沿AB匀速运动；点Q从点C出发，沿CB匀速运动.两点同时出发，在B点处首次相遇.设点P的速度为xcm/s. 表示点Q的速度是多少cm/s（用含的代数式表示）；

    （2）在（1）的条件下，两点在B点处首次相遇后，点P的运动速度每秒提高了2 cm，并沿B→C→A的路径匀速运动；点Q保持原速度不变，沿B→A→C的路径匀速运动，如图2.两点在AC边上点D处再次相遇后停止运动.又知AD=1cm.求点P原来的速度x的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB的延长线于G．

    （1）求证：AEFD=AFEC；

    （2）求证：FC=FB；

    （3）若FB=FE=2，求⊙O的半径r的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抚顺某中学为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级．请根据两幅统计图中的信息回答下列问题：

    （1）本次抽样调查共抽取了多少名学生？

    （2）求测试结果为C等级的学生数，并补全条形图；

    （3）若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名？

    （4）若从体能为A等级的2名男生2名女生中随机的抽取2名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．

    ⑴若∠AFD=155°，求∠EDF的度数；

    ⑵若点F是AC的中点，求证：∠CFD=∠B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

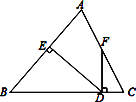
    【题目】如图，在△ABC中，D是BC的中点，过D点的直线EG交AB于点E，交AB的平行线CG于点G，DF⊥EG，交AC于点F．

    （1）求证：BE=CG；

    （2）判断BE+CF与EF的大小关系，并证明你的结论．

    查看答案和解析>>

    同步练习册答案