
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.

(1)出发2秒后,求![]() 的周长.
的周长.
(2)问![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分?
的两部分?
【答案】(1)![]() cm;(2)当
cm;(2)当![]() 为3秒、5.4秒、6秒、6.5秒时,
为3秒、5.4秒、6秒、6.5秒时,![]() 为等腰三角形;(3)
为等腰三角形;(3)![]() 或
或![]() 或
或![]() 秒
秒
【解析】
(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长;
(2)分点P在边AC上和点P在边AB上两种情况求解即可;
(3)分类讨论:①当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上;②当
上;②当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上;③当
上;③当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上.
上.
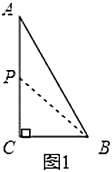
解:(1)如图1,由![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,
,
∴出发2秒后,则![]() ,
,
∴AP=2,
∵![]() ,
,
∴![]() ,
,
∴![]() 的周长为:
的周长为:![]() .
.
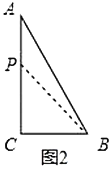
(2)①如图2,若![]() 在边
在边![]() 上时,
上时,![]() ,
,
此时用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
②2若![]() 在
在![]() 边上时,有三种情况:
边上时,有三种情况:
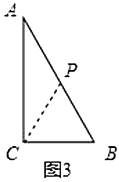
(ⅰ)如图3,若使![]() ,此时
,此时![]() ,
,![]() 运动的路程为
运动的路程为![]() ,
,
所以用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
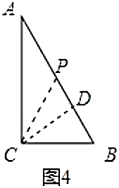
(ⅱ)如图4,若![]() ,作
,作![]() 于点
于点![]() ,
,
∵![]() ,
,
∴CD=![]() ,
,
在![]() 中,
中,
![]() ,
,
所以![]() ,
,
所以![]() 运动的路程为
运动的路程为![]() ,
,
则用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
(ⅲ)如图5,若![]() ,此时
,此时![]() 应该为斜边
应该为斜边![]() 的中点,
的中点,![]() 运动的路程为
运动的路程为![]() ,
,
则所用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
综上所述,当![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 时,
时,![]() 为等腰三角形;
为等腰三角形;
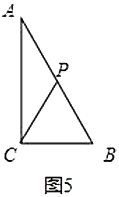
(3)①3÷2=1.5秒,如图6,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
∴![]() ,∴
,∴![]() ,符合题意;
,符合题意;
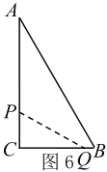
②(3+5) ÷2=4秒,如图7,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
∴![]() ,
,![]() ,符合题意;
,符合题意;
③12÷2=6秒,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
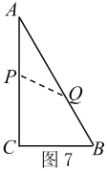
(ⅰ)当AP+AQ=周长的![]() 时,如图8,
时,如图8,
∴![]() ,
,![]() ,符合题意;
,符合题意;
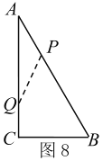
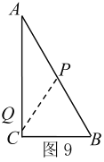
(ⅱ)当AP+AQ=周长的![]() 时,如图9,
时,如图9,
∴![]() ,∴
,∴![]() ;
;
∵当![]() 秒时,点
秒时,点![]() 到达
到达![]() 点停止运动,
点停止运动,
∴![]() 这种情况应该舍去.
这种情况应该舍去.
综上,当![]() 为
为![]() 或
或![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分.
的两部分.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如下两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
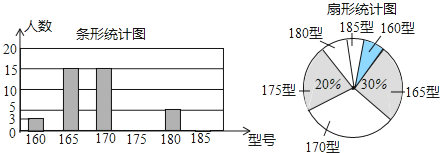
根据以上信息,解答下列问题:
(Ⅰ)该班共有 名学生,其中穿175型校服的学生有 名;
(Ⅱ)在条形统计图中,请把空缺部分补充完整.
(Ⅲ)在扇形统计图中,185型校服所对应的扇形圆心角的大小为 ;
(Ⅳ)该班学生所穿校服型号的众数为 ,中位数为 .
(Ⅴ)如果该校预计招收新生600名,根据样本数据,估计新生中穿170型校服的学生大约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
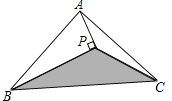
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
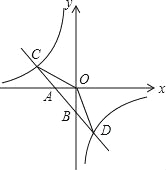
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线![]() :
:![]() (a≠0),
(a≠0),
(1)试求抛物线![]() 的函数解析式;
的函数解析式;
(2)求证: 抛物线 ![]() 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;
(3)若a=1
①抛物线![]() 、
、![]() 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
②已知直线MN分别与x轴、![]() 、
、![]() 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com