
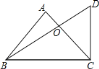
【题目】一副三角板如图所示放置,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】
根据题意得出各角的度数,进而利用锐角三角函数关系得出DF,FC,AO,AB,FO的长,进而表示出两三角形面积求出即可.
∵一副三角板如图所示放置,
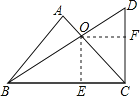
∴过点O作OE⊥BC于点E,作OF⊥DC于点F,
∵∠ACB=45°,∠BCD=90°,
∴∠ACB=∠ACD=45°,∠D=60°,∠DBC=30°,
∴EO=EC=FO=FC,
设EO=EC=FO=FC=x,
∴DF=FOtan60°=![]() x,
x,
CO=![]() x,BE=
x,BE=![]() x,
x,
∴AB=![]() (
(![]() x+x)=
x+x)=![]() ,
,
故AO=![]() =
=![]() ,
,
∴S△ABO=![]() ×AO×AB=
×AO×AB=![]() ×
×![]() ×
×![]() =
=![]() x2,
x2,
S△DOC=![]() ×FO×CD=
×FO×CD=![]() x(x+
x(x+![]() x)=
x)=![]() ×
×![]() x2,
x2,
∴S△ODC:S△AOB的值为:![]() ×
×![]() x2:
x2:![]() x2=
x2=![]() .
.
故答案为:![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方,在原点的上方.下列结论:①4a﹣2b+c=0;②2a﹣b<0;③2a﹣b>﹣1;④2a+c<0;⑤b>a;其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某服装厂现有![]() 种布料70米,
种布料70米,![]() 种布料52米,现计划用这两种布料生产
种布料52米,现计划用这两种布料生产![]() 、
、![]() 两种型号的时装共80套.已知做一套
两种型号的时装共80套.已知做一套![]() 型号的时装需用A种布料1.1米,
型号的时装需用A种布料1.1米,![]() 种布料0.4米,可获利50元;做一套
种布料0.4米,可获利50元;做一套![]() 型号的时装需用
型号的时装需用![]() 种布料0.6米,
种布料0.6米,![]() 种布料0.9米,可获利45元.设生产
种布料0.9米,可获利45元.设生产![]() 型号的时装套数为
型号的时装套数为![]() ,用这批布料生产两种型号的时装所获得的总利润为
,用这批布料生产两种型号的时装所获得的总利润为![]() 元.
元.
(1)求![]() (元)与
(元)与![]() (套)的函数关系式.
(套)的函数关系式.
(2)有几种生产方案?
(3)如何生产使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.

(1)出发2秒后,求![]() 的周长.
的周长.
(2)问![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分?
的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
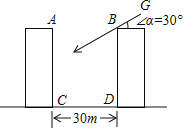
【题目】两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.
(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?
(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.
查看答案和解析>>
科目:初中数学 来源: 题型:
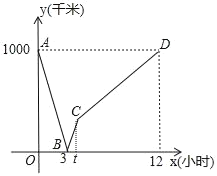
【题目】一列动车从A地开往B地,一列普通列车从B地开往A地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系,下列说法中正确的是:( )
①AB两地相距1000千米;②两车出发后3小时相遇;③普通列车的速度是100千米/小时;④动车从A地到达B地的时间是4小时.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,两锐角的度数之比为2:1,其最短边为1,射线CP交AB所在的直线于点P,且∠ACP=30°,则线段CP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com