
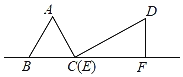
【题目】如图,在Rt△DEF中,∠EFD=90°,∠DEF=30°,EF=3cm,边长为2cm的等边△ABC的顶点C与点E重合,另一个顶点B(在点C的左侧)在射线FE上.将△ABC沿EF方向进行平移,直到A、D、F在同一条直线上时停止,设△ABC在平移过程中与△DEF的重叠面积为ycm2,CE的长为xcm,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
B.
C.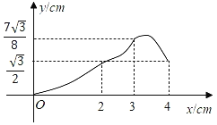 D.
D.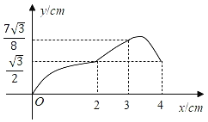
【答案】A
【解析】
分0≤x≤2、2<x≤3、3<x≤4三种情况,分别求出函数表达式即可求解.
解:①当0≤x≤2时,如图1,
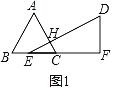
设AC交ED于点H,则EC=x,
∵∠ACB=60°,∠DEF=30°,
∴∠EHC=90°,
y=S△EHC=![]() ×EH×HC=
×EH×HC=![]() ECsin∠ACB×EC×cos∠ACB=
ECsin∠ACB×EC×cos∠ACB=![]() CE2=
CE2=![]() x2,
x2,
该函数为开口向上的抛物线,当x=2时,y=![]() ;
;
②当2<x≤3时,如图2,
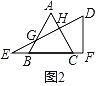
设AC交DE于点H,AB交DE于点G,
同理△AHG为以∠AHG为直角的直角三角形,
EC=x,EB=x﹣2=BG,则AG=2﹣BG=2﹣(x﹣2)=4﹣x,
边长为2的等边三角形的面积为:![]() 2×
2×![]() =
=![]() ;
;
同理S△AHG=![]() (4﹣x)2,
(4﹣x)2,
y=S四边形BCHG=S△ABC﹣S△AHG=![]() ﹣
﹣![]() (x﹣4)2,
(x﹣4)2,
函数为开口向下的抛物线,当x=3时,y=![]() ,
,
③当3<x≤4时,如图3,
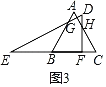
同理可得:y=![]() ﹣[
﹣[![]() (4﹣x)2+
(4﹣x)2+![]() (x﹣3)2]=﹣
(x﹣3)2]=﹣![]() x2+4
x2+4![]() x﹣
x﹣![]() ,
,
函数为开口向下的抛物线,当x=4时,y=![]() ;
;
故选:A.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
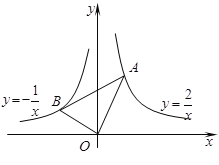
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
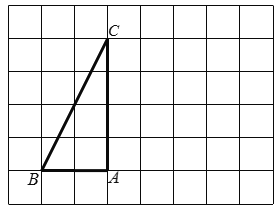
【题目】如图,在每个小正方形的边长为![]() 的网格中,△
的网格中,△![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(1)![]() 的长等于_____________;
的长等于_____________;
(2)在如图所示的网格中,将△![]() 绕点
绕点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,得到△
上,得到△![]() ,请用无刻度的直尺,画出△
,请用无刻度的直尺,画出△![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期复学后,学校为了保障学生的出行安全,随机调查了部分学生的上学方式(每位学生从乘私家车、坐公交、骑车和步行4种方式中限选1项),根据调查数据制作了如图所示的不完整的统计表和扇形统计图.

(1)本次学校共调查了 名学生,![]() ,
,![]() ;
;
(2)求扇形统计图中“步行”对应扇形的圆心角;
(3)甲、乙两位同学住在同一小区,且都坐公交车上学,有![]() 、
、![]() 、
、![]() 三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
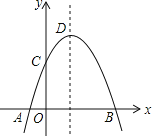
【题目】如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①抛物线的对称轴是直线x=1;
②若OC=OB,则c=2;
③若M(x0,y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.其中真命题个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③![]() .
.
其中正确的是

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
A.直角三角形B.平行四边形C.菱形D.等腰梯形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com