
【题目】在平面直角坐标系中,过格点A、B、C作一圆弧.
(1)弧AC的长为_____(结果保留π);
(2)点B与图中格点的连线中,能够与该圆弧相切的连线所对应的格点的坐标为_____.

【答案】(1)![]() (2)(5,1)或(1,3)或(7,0)
(2)(5,1)或(1,3)或(7,0)
【解析】
(1)根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心,然后根据弧长的公式即刻得到结论;
(2)由弦AB与弦BC的垂直平分线的交点为圆心,找出圆心O′的位置,确定出圆心坐标,过点B与圆相切时,根据切线的判定方法得到∠O′BF为直角时,BF与圆相切,根据网格找出满足条件的F坐标即可.
(1)根据过格点A,B,C作一圆弧,
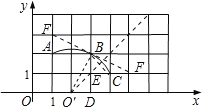
由图形可得:三点组成的圆的圆心为:O′(2,0),
∴半径![]()
连接![]()
则![]()
∴弧AC的长![]()
故答案为:![]()
(2)∵由图形可得:三点组成的圆的圆心为:O′(2,0),
∴只有![]() 时,BF与圆相切,
时,BF与圆相切,
此时△BO′D≌△FBE,EF=BD=2,
∴F点的坐标为:(5,1)或(1,3)或(7,0),
则点B与下列格点的连线中,能够与该圆弧相切的是(5,1)或(1,3)或(7,0),共3个.
故答案为:(5,1)或(1,3)或(7,0).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE,CE.则CE=___________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为2km和7km,且张、李二村庄相距13km.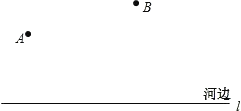
(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
(2)如果铺设水管的工程费用为每千米1500元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在Rt△ABC的斜边AB上,且AC=6,
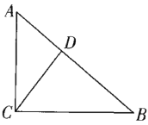
(1) 若AB比BC大2,①求AB的长;②若CD⊥AB于点D,求CD的长.
(2)若AD=7,DB=11, ∠CDB=2∠B,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)感知:如图(1),在△ABC中,分别以AB、AC为边在△ABC外部作等边三角形△ABD、△ACE,连接CD、BE.求证:BE=DC;
(2)应用:如图(2),在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰三角形△ABD、△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为25cm2,求△ABE的面积.
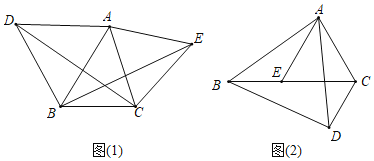
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com