
【题目】如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为2km和7km,且张、李二村庄相距13km.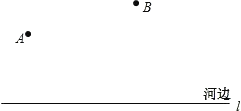
(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
(2)如果铺设水管的工程费用为每千米1500元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?
【答案】(1)详见解析;(2)22500
【解析】
(1)作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置;
(2)利用了轴对称的性质可得AP=A′P,在△AEB中利用勾股定理可以算出AE的长,再在△ACB中利用勾股定理算出A′B的长,根据两点之间线段最短的性质即可求解.
(1)作A关于l的对称点A′,再连接A′B,A′B与l交于点P,P点就是水泵站的位置;
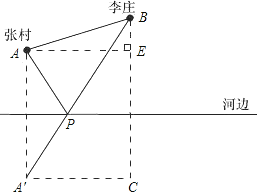
(2)过B点作l的垂线,过A′作l的平行线,
设这两线交于点C,则∠C=90°.
又过A作AE⊥BC于E,
依题意BE=5,AB=13,
∴AE2=AB2-BE2=132-52=144.
∴AE=12.
由平移关系,A′C=AE=12,
△BA′C中,
∵BC=7+2=9,A′C=12,
∴A′B2=A′C2+BC2=92+122=225,
∴A′B=15.
∵PA=PA′,
∴PA+PB=A′B=15.
∴1500×15=22500(元).
答:最节省的铺设水管的费用为22500元


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将![]() 绕点A顺时针旋转到
绕点A顺时针旋转到![]() 的位置,点B、O分别落在点
的位置,点B、O分别落在点![]() 、
、![]() 处,点
处,点![]() 在x轴上,再将
在x轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,将
在x轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,依次进行下去
在x轴上,依次进行下去![]() 若点
若点![]() ,
,![]() ,则点
,则点![]() 的坐标为______.
的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数关系式;
(2)判断点(-5,3)是否在此函数的图象上,说明理由;
(3)求出该函数图像与坐标轴围成的三角形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形的绿地,量得两直角边长分别为5m,12m.现在要将绿地扩充成等腰三角形绿地,且扩允部分是以12m为直角边的直角三角形,求扩充部分三角形绿地的面积.(如图备用)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90 ,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
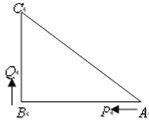
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过格点A、B、C作一圆弧.
(1)弧AC的长为_____(结果保留π);
(2)点B与图中格点的连线中,能够与该圆弧相切的连线所对应的格点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() 。
。
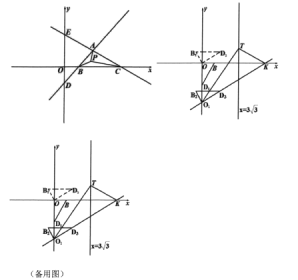
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)将点![]() 向下平移一个单位得到点
向下平移一个单位得到点![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() 的位置,使
的位置,使![]() 轴,再将
轴,再将![]() 沿
沿![]() 轴上下平移得到
轴上下平移得到![]() ,在平移过程中,直线
,在平移过程中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 能否以
能否以![]() 为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的
为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的![]() 点的坐标,若不能,请说明理由。
点的坐标,若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com