
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() 。
。
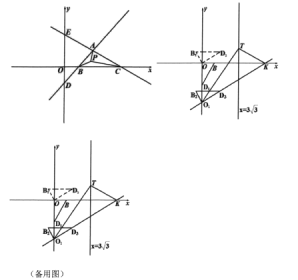
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)将点![]() 向下平移一个单位得到点
向下平移一个单位得到点![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() 的位置,使
的位置,使![]() 轴,再将
轴,再将![]() 沿
沿![]() 轴上下平移得到
轴上下平移得到![]() ,在平移过程中,直线
,在平移过程中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 能否以
能否以![]() 为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的
为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的![]() 点的坐标,若不能,请说明理由。
点的坐标,若不能,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)T1
;(3)T1![]() ,T2(
,T2(![]() ),T3(
),T3(![]() )
)
【解析】
(1)列方程组求两个一次函数的交点坐标;(2)将△APC绕点C顺时针旋转60°,得到△DEC,连接BE,PD,则线段BE即为PA+PB+PC最小值的线段;(3)分四种情形:①当O1K=KT时,且O1在x轴下方,②当O1K=O1T时,且O1在x轴下方,③当O1K=KT时,且O1在x轴上方,④当O1K=O1T时,且O1在x轴上方,逐个进行计算即可.
解:(1)由题意可得:
解得:
∴点A的坐标为![]()
(2)如图2,将△APC绕点顺时针旋转60°得到△EDC,连接BE,PD.

在![]() 中
中
当x=0时,y=4
当y=0时,![]()
∴![]()
∴∠ACB=30°
由旋转的性质可知:△PCD是等边三角形,
∴PC=PD,
∵PA=DE,
∴PA+PB+PC=DE+PB+PD,
∵DE+PB+PD≥BE,
∴当P,D在直线BE上时,PA+PB+PC的值最小,
∵在![]() 中
中
当y=0时,![]()
∴BC=CE=![]() ,∠BCE=90°,
,∠BCE=90°,
∵EB⊥BC,
∴BE=![]() BC=
BC=![]() ,
,
∴PA+PB+PC的最小值为![]() .
.
(3)①当O1K=KT时,且O1在x轴下方,如图,则M(![]() )
)
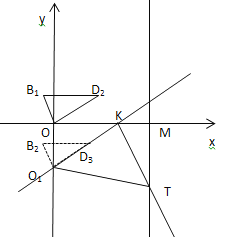
由题意可知:OB=OB1=![]() ,OD=2,OD1=3
,OD=2,OD1=3
∴![]()
∴∠OKO1=30°
∵![]() 是等腰直角三角形
是等腰直角三角形
∴易证:△KTM≌△O1OK
∴OK=MT
设MT=t,则KM=![]()
∴![]()
解得:![]()
∴T点坐标为(![]() )
)
②当O1K=O1T时,且O1在x轴下方,如图,作TN⊥y轴于N,

∵∠KON=∠TNO=∠TO1K=90°,
∴∠OO1K+∠O1KO=∠OO1K+∠TO1N=90°
∴∠O1KO=∠TO1N
∵O1K=O1T
∴△O1KO≌△TO1N(AAS)
∴OO1=TN=![]()
∵∠OKO1=30°
即:![]()
∴O1N=OK=9
∴ON=![]()
∴T2(![]() ),
),
③当O1K=KT时,且O1在x轴上方,方法同①,此时,点T不存在;
④当O1K=O1T时,且O1在x轴上方,方法同②,可求得T3(![]() );
);
综上所述,使△O1KT成为以O1K为直角边的等腰直角三角形的点T的坐标为:T1![]() ,T2(
,T2(![]() ),T3(
),T3(![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为2km和7km,且张、李二村庄相距13km.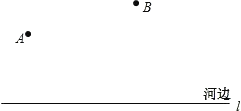
(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
(2)如果铺设水管的工程费用为每千米1500元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k,b,则一次函数y=kx+b的图象不经过第四象限的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com