练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为
     
    ．
    考点：抛物线与x轴的交点
    专题：
    分析：由二次函数y=-x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标，然后可以求出另一个交点坐标，再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程-x2+2x+m=0的解．
    解答：解：依题意得二次函数y=-x2+2x+m的对称轴为x=1，与x轴的一个交点为（3，0），
    ∴抛物线与x轴的另一个交点横坐标为1-（3-1）=-1，
    ∴交点坐标为（-1，0）
    ∴当x=-1或x=3时，函数值y=0，
    即-x2+2x+m=0，
    ∴关于x的一元二次方程-x2+2x+m=0的解为x1=-1或x2=3．
    故答案为：x1=-1或x2=3．
    点评：本题考查的是关于二次函数与一元二次方程，在解题过程中，充分利用二次函数图象，根据图象提取有用条件来解答，这样可以降低题的难度，从而提高解题效率．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，△ABC中，AD⊥BC于D，下列条件：（1）∠B+∠DAC=90°；（2）∠B=∠DAC；（3）
    CD
    AD
    =
    AC
    AB
    ；（4）AB2=BD•BC．其中一定能够判定△ABC是直角三角形的有（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读下面的材料：
    1×2=
    1
    3
    （1×2×3-0×1×2），
    2×3=
    1
    3
    （2×3×4-1×2×3），
    3×4=
    1
    3
    （3×4×5-2×3×4）
    由以上三个等式相加可得
    1×2+2×3+3×4=
    1
    3
    ×3×4×5=20
    根据以上材料，请你计算下列各题：
    （1）1×2+2×3+3×4+…+10×11（写出过程）；
    （2）1×2+2×3+3×4+…+n（n+1）=
    （3）模仿上面的材料，试计算1×2×3+2×3×4+3×4×5+…+10×11×12的结果（写过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    日军从1937年12月13日攻占南京开始持续了6周，在南京犯下了大规模屠杀强奸纵火抢劫等战争罪行和反人类罪行，其中屠杀我同胞大约300000人，用科学记数法表示该数据为
     
    人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察下列各式计算结果：
    1-
    1
    22
    =1-
    1
    4
    =
    3
    4
    =
    1
    2
    ×
    3
    2

    1-
    1
    32
    =1-
    1
    9
    =
    8
    9
    =
    2
    3
    ×
    4
    3

    1-
    1
    42
    =1-
    1
    16
    =
    15
    16
    =
    3
    4
    ×
    5
    4

    1-
    1
    52
    =1-
    1
    25
    =
    24
    25
    =
    4
    5
    ×
    6
    5

    （1）用你发现的规律填写下列式子的结果：
    1-
    1
    102
    =
     
    .1-
    1
    1002
    =
     
    .1-
    1
    20142
    =
     
    ．
    （2）用你发现的规律计算：
    （1-
    1
    22
    ）×（1-
    1
    32
    ）×（1-
    1
    42
    ）×…×（1-
    1
    20132
    ）×（1-
    1
    20142
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

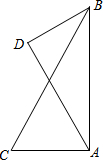    如图，一艘科学考察船由港口A出发沿正北方向航行，在航线的一侧有两个小岛C、D．考察船在A处时，测得小岛C在船的正西方，小岛D在船的北偏西30°方向．考察船向北航行了12千米到B处时，测得小岛C在船的南偏西30°方向，小岛D在船的南偏西60°方向．求小岛C、D之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，抛物线y=ax2+bx+c与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C（0，-3）
    （1）求抛物线的解析式；
    （2）在x轴下方的抛物线上是否存在在一点D，使四边形ABCD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；
    （3）在抛物线y=ax2+bx+c上求点E，使△BCE是以BC为直角边的直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    同时抛掷两枚质地均匀的骰子，骰子的六个面分别刻有1到6的点数，朝上的面的点数中，一个点数能被另一个点数整除的概率是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，菱形ABCD中，若∠ABC=120°，BD=1，则AC=
     
    ．

    查看答案和解析>>

    同步练习册答案