
【题目】如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )

A. 5对 B. 6对 C. 7对 D. 8对
【答案】A
【解析】解:①在△AEO与△ADO中,∵AE=AD,∠1=∠2,OA=OA,∴△AEO≌△ADO(SAS);
②∵△AEO≌△ADO,∴OE=OD,∠AEO=∠ADO,∴∠BEO=∠CDO.
在△BEO与△CDO中,∵∠BEO=∠CDO,OE=OD,∠BOE=∠COD,∴△BEO≌△CDO(ASA);
③∵△BEO≌△CDO,∴BE=CD,BO=CO,OE=OD,∴CE=BD.
在△BEC与△CDB中,∵BE=CD,∠BEC=∠CDB,CE=BD,∴△BEC≌△CDB(SAS);
④在△AEC与△ADB中,∵AE=AD,∠AEC=∠ADB,CE=BD,则△AEC≌△ADB(SAS);
⑤∵△AEC≌△ADB,∴AB=AC.
在△AOB与△AOC中,∵AB=AC,OB=OC,OA=OA,∴△AOB≌△AOC.
综上所述,图中全等三角形共5对.
故选A.


科目:初中数学 来源: 题型:
【题目】感知:
(1)如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
(2)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
(3)拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ![]() ,CE=3,则DE的长为 .
,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):
根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
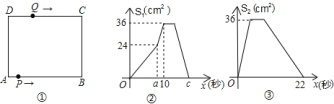
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,到
运动,到![]() 点停止.若点
点停止.若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() .如图
.如图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象;图
(秒)的函数关系图象;图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象:
![]() 求
求![]() 、
、![]() 、
、![]() 的值;
的值;
![]() 设点
设点![]() 出发
出发![]() (秒)后离开点
(秒)后离开点![]() 的路程为
的路程为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足. 
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB. 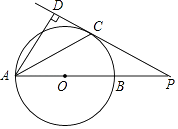
(1)求证:AD⊥PC;
(2)连接BC,如果∠ABC=60°,BC=2,求线段PC的长. 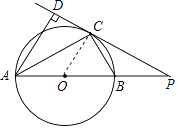
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com