
����Ŀ���й��и����䡰�˳���֮�У���ʤǧ��֮�⡱�����еġ��ԭ����ָ�������㾭���м��صġ���������ǹŴ��������м���Ĺ��ߣ����ǽ����糤��С�������ƽ���Ͻ������㣬���İڷ���ʽ���ݺ�������ʽ����ͼ����

����ʾһ����λ��ʱ������������һ�����Ѹ�����λ��������������У�����λ����ij�ʽ��Ҫ�ݺ���䣺��λ����λ����λ������ʽ��ʾ��ʮλ��ǧλ��ʮ��λ���ú�ʽ��ʾ����0���ÿ�λ�����棬�Դ����ƣ�����3306������ʾ����![]() ����2022�����ɱ�ʾΪ�� ��
����2022�����ɱ�ʾΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͬѧ��Ӧ�����������˶������٣����ÿ��������μ�����������ÿλͬѧ�ӳ��ܡ�Ǧ��������Զ������Ͷ������ѡһ�������ѵ����ѵ��ǰ�����˲��ԣ��ֽ���Ŀѡ�������ѵ��������Ͷ��������������������������ͳ��ͼ����
ѵ��������Ͷ�����Խ���ͳ�Ʊ���
������������ | 8 | 7 | 6 | 5 | 4 | 3 |
���� | 2 | 1 | 4 | 7 | 8 | 2 |
��1��ѡ����ѵ��������ռȫ�������İٷֱ����� �����ð��ͬѧ�� ���ˣ�
��2����ѵ��������Ͷ���˾�������Ϊ���ٸ���
��3�����ݲ������ϣ��μ�����Ͷ����ѧ��ѵ�����ѵ��ǰ���˾�����������25%����μ�ѵ��֮ǰ���˾���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��B�����Ӧ���������ֱ���![]() ��15����ֻ�������ϼף��ҷֱ��A��B����ͬʱ����������У����ٶ���3����λ/�룬�ҵ��ٶ���6����λ/��
��15����ֻ�������ϼף��ҷֱ��A��B����ͬʱ����������У����ٶ���3����λ/�룬�ҵ��ٶ���6����λ/��
��1�����ҵ���A��ʱ���������λ�ö�Ӧ������
��2����������������![]() ��ף�������λ�ö�Ӧ�����ֱ��Ƕ��٣����ú�
��ף�������λ�ö�Ӧ�����ֱ��Ƕ��٣����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��3����������������![]() ��
��![]() ����ף��������ٸ���λ�����ú�
����ף��������ٸ���λ�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������ĸ����ء���ľ֮����֮�������־ͷ�������������ξ�����е��飬A������ͤ�ֺ�����B�������ӹ�������C��������ɽ����ɭ�ֹ�����D����С��ׯ����E�����������ʾ�����Ϊ�˽�ѧ����ϲ����һ�����㣨ÿ��ֻѡȡһ�֣��������ȡ�˲���ѧ�����е��飬�����������Ƴ����²�������ͳ�Ʊ���ͳ��ͼ������������Ϣ����������⣺


��1�����ν��ܵ����������Ϊ______�ˣ�ͳ�Ʊ���m=______��n=______��
��2����ȫ����ͳ��ͼ��
��3����������ͳ��ͼ��Ϊ����ͳ��ͼ����������ɽ����ɭ�ֹ�������С��ׯ�������������ʾ����������ε�Բ�ĽǶ����ֱ���__________��___________��___________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ĶԽ���AC��������ԭ��O�����εı߷ֱ�ƽ���������ᣬ��B�ں���![]() ��k��0��x��0����ͼ���ϣ���D������Ϊ����4��1������k��ֵΪ��������
��k��0��x��0����ͼ���ϣ���D������Ϊ����4��1������k��ֵΪ��������
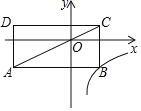
A.![]() B.
B.![]() C.4D.��4
C.4D.��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨��������![]() �������ϵ�
�������ϵ�![]() ��ʾ��
��ʾ��![]() ������
������![]() �������ϵ����ꣻ������
�������ϵ����ꣻ������![]() �������ϵ�
�������ϵ�![]() ��ʾ��
��ʾ��![]() ������
������![]() �������ϵ�����.
�������ϵ�����.![]() ��ʾ�����ϵ�����
��ʾ�����ϵ�����![]() ��
��![]() ֮��ľ���.
֮��ľ���.
��1���������ᣬ����±���
|
|
|
|
3 | 2 | 1 | 1 |
1 | 5 | ______ | ______ |
2 | ��3 | ______ | ______ |
��4 | 1 | ______ | ______ |
��5 | ��2 | ______ | ______ |
��3 | ��6 | ______ | ______ |
��2���۲죨1���еı������ݣ�����![]() ______�����ú�
______�����ú�![]() ��
��![]() ��ʽ�ӱ�ʾ������˵����
��ʽ�ӱ�ʾ������˵����
��3����֪��![]() �������ϵ������ǣ�2����
�������ϵ������ǣ�2����![]() �����ã�2���еĽ������
�����ã�2���еĽ������![]() �������ϵ�����.
�������ϵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OM��������A��B��C��OC=45cm, BC=15cm, AB=30cm����֪����P��Qͬʱ�˶������ж���P�ӵ�O������OM�������ٶ�2cm/s�����˶�������Q�ӵ�C������CA���������˶�������Q�˶�����Aʱ����Qֹͣ�˶�����P�����˶���.���˶�ʱ��Ϊt��.

��1�����P�˶�����B���õ�ʱ�䣻
��2������Q�˶��ٶ�Ϊÿ��1cm������������ʱ����P�͵�Q�ľ���Ϊ30cm��
��3����PA=2PBʱ����Qǡ�����߶�AB�����ȷֵ��λ�ã����Q���ٶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016���������У���֪���������ε����߳�������������������
��ϣ���ļ���ѧ�Һ������������⣬�����������������ۡ�һ���и����˼��㹫ʽ��������ʽS=![]() ������a��b��c�������ε����߳���p=
������a��b��c�������ε����߳���p=![]() ��SΪ�����ε����������������֤��
��SΪ�����ε����������������֤��
���磺����ABC�У�a=3��b=4��c=5����ô������������������㣺
��a=3��b=4��c=5����p=![]() =6����S=
=6����S=![]() =
=![]() =6��
=6��
��ʵ�ϣ�������֪�����ε����߳�����������������⣬�������ҹ�����ʱ����ѧ���ؾ���������ؾ��ع�ʽ�ȷ��������
��ͼ������ABC�У�BC=5��AC=6��AB=9
��1���ú���ʽ����ABC�������
��2������ABC������Բ�뾶r��
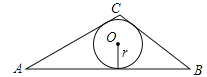
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������֪��ֽ������һ����(��ͼ��ʾ).
![]()
�����۵�ֽ�棬�ۺ����ڵ�ֱ��������Ľ���Ϊ���������ĵ���
����һ��
(1)�����۵�ֽ�棬ʹ1��ʾ�ĵ���-1��ʾ�ĵ��غϣ���-3��ʾ�ĵ��� ��ʾ�ĵ��غϣ�
��������
(2)�����۵�ֽ�棬ʹ-1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
�ٶ������ĵ�����ʾ����Ϊ ,���ۺ�5��ʾ�ĵ����� ��ʾ�ĵ��غϣ�
����������A.B����֮�����Ϊ11��A��B����ࣩ����A.B���㾭�۵����غϣ���A.B�����ʾ�����Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com