
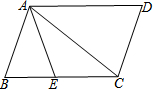
 如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1.
如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1. 分析 由?ABCD的性质及∠BAE=∠DAC可得∠BAE=∠BCA,进而可判定△BAE∽△BCA,根据对应边成比例可得$\frac{BA}{BC}=\frac{BE}{BA}$即$\frac{7}{10}=\frac{10-EC}{7}$,解之即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC=10,
∴∠DAC=∠BCA,
又∵∠BAE=∠DAC,
∴∠BAE=∠BCA,
∵∠B=∠B,
∴△BAE∽△BCA,
∴$\frac{BA}{BC}=\frac{BE}{BA}$,
∵AB=7,BC=10,
∴$\frac{7}{10}=\frac{10-EC}{7}$,
解得:EC=5.1.
故答案为:5.1.
点评 本题主要考查相似三角形的判定及性质、平行四边形的性质,根据平行四边形的性质得到∠BAE=∠BCA是判定三角形相似的前提,熟练运用相似形的性质是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
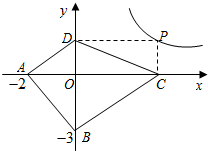
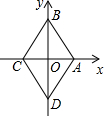 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
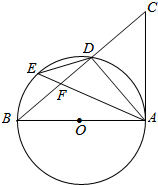 如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.
如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
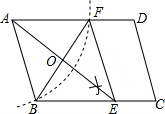 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
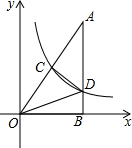 如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.
如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com