
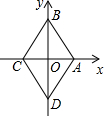
 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$). 分析 先根据勾股定理求出菱形的边长,再根据点P的运动速度求出沿A→B→C→D→A所需的时间,进而可得出结论.
解答 解:∵A(1,0),B(0,$\sqrt{3}$),
∴AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间=$\frac{2}{0.5}$=4(秒),
∴沿A→B→C→D→A所需的时间=4×4=16秒.
∵$\frac{2017}{16}$=126…1,
∴移动到第2017秒和第1秒的位置相同,当P运动到第1秒时,如图所示,可得,$\frac{AP}{AB}$=$\frac{1}{4}$,
如图所示,根据相似的性质可知,$\frac{PE}{OB}$=$\frac{AP}{AB}$,$\frac{PF}{AO}$=$\frac{BP}{AB}$,
则$\frac{PE}{\sqrt{3}}$=$\frac{1}{4}$,$\frac{PF}{1}$=$\frac{3}{4}$,
解得:PE=$\frac{\sqrt{3}}{4}$,PF=$\frac{3}{4}$,
故点P的坐标为:($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
故答案为:($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
点评 本题考查的是菱形的性质,根据题意得出点P运动一周所需的时间是解答此题的关键.


科目:初中数学 来源: 题型:解答题
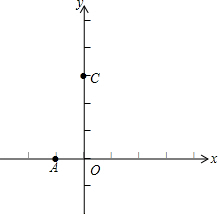 在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.
在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
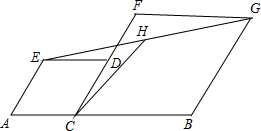 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
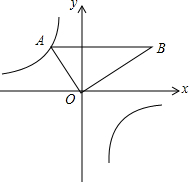 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com