
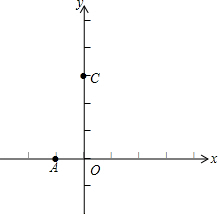
 在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.
在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.分析 (1)将点A(-1,0)代入抛物线的解析式可求得b的值,然后可得到抛物线的解析式,从而可求得抛物线的对称轴,再依据对称性可求得D(2,3),B(3,0),最后依据待定系数法求得AD的解析式可求得直线AD与x轴正方向的夹角;
(2)设E(m,-m2+2m+3),则F(-m2+2m+2,-m2+2m+3),EF=-m2+m+2.然后证明△EFG为等腰直角三角形,从而得到EF=(1+$\sqrt{2}$)EF,于是可求得l与m的关系式;
(3)先利用配方法求得点M的坐标,然后根据①AM为矩形的对角线时,②当AM为矩形的一边时两种情况求解即可.
解答 解:(1)∵将点A(-1,0)代入抛物线的解析式得:-1-b+3=0,解得:b=2,
∴y=-x2+2x+3.
∴抛物线的对称轴为直线x=1.
令x=0得:y=3,则C(0,3).
∵点B与点A、点D与点C分别关于该抛物线的对称轴对称,
∴D(2,3),B(3,0).
设直线AD的解析式为y=kx+b.
∵将A(-1,0)、D(2,3)代入得:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=3}\end{array}\right.$,解得:k=1,b=1,
∴直线AD的解析式为y=x+1.
∴直线AD与x轴正方向的夹角为45°.
(2)如图1所示: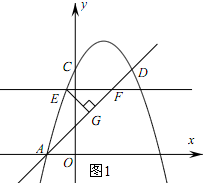
设E(m,-m2+2m+3),则F(-m2+2m+2,-m2+2m+3),EF=-m2+2m+2-m=-m2+m+2.
∵∠EGF=90°,∠EFG=45°,
∴△EFG为等腰直角三角形.
∴l=EF+FG+EG=EF+$\frac{\sqrt{2}}{2}$EF+$\frac{\sqrt{2}}{2}$EF=(1+$\sqrt{2}$)EF=(1+$\sqrt{2}$)(-m2+m+2)=-($\sqrt{2}+1$)m2+($\sqrt{2}$+1)m+2$\sqrt{2}$+2.
(3)∵y=-x2+2x+3=-(x-1)2+4,
∴M(1,4).
①AM为矩形的对角线时,如图2所示: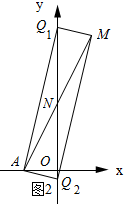
∵由矩形的性质可知:N为AM的中点,A(-1,0),M(1,4),
∴N(0,2).
∵由两点间的距离公式可知:MN=$\sqrt{(1-0)^{2}+(4-2)^{2}}$=$\sqrt{5}$.
∴NQ1=NQ2=$\sqrt{5}$,
∴Q1(0,2+$\sqrt{5}$),Q2(0,2-$\sqrt{5}$).
②当AM为矩形的一边时,如图3所示:过Q3作Q3E⊥y轴,垂直为E,过Q4作Q4F⊥y轴,垂足为F.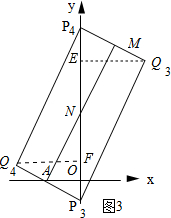
∵在△ANO中,AO=1,ON=2,
∴tan∠ANO=$\frac{1}{2}$,
∴tan∠MNP4=$\frac{1}{2}$,
∴P4M$\frac{1}{2}$MN=$\frac{\sqrt{5}}{2}$,NP4=$\frac{\sqrt{5}}{2}$MN=$\frac{5}{2}$.
∴P4Q3=$\sqrt{5}$.
∴P4E=$\frac{\sqrt{5}}{5}$P4Q3=1,EQ3=$\frac{2\sqrt{5}}{5}$P4Q3=2.
∵OE=OP4-P4E=4.5-1=3.5,
∴Q3的坐标为(2,3.5).
∵点Q3与Q4关于点N对称,
∴Q4(-2,$\frac{1}{2}$).
综上所述,点Q的坐标为(0,2+$\sqrt{5}$),或(0,2-$\sqrt{5}$)或(2,3.5)或(-2,$\frac{1}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、配方法求抛物线的顶点坐标、矩形的性质、锐角三角函数的定义,根据题意画出符合题意的图形是解题的关键.


科目:初中数学 来源: 题型:解答题
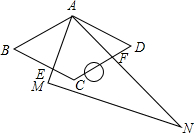 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
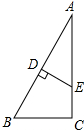 如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.
如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
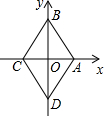 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2017秒时,点P的坐标为($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com