
����Ŀ����ͼ1����֪������y��x2+bx��3��b�dz�������x�ύ��A��B���㣬��y�ύ�ڵ�C���ҵ�A����Ϊ����1��0����
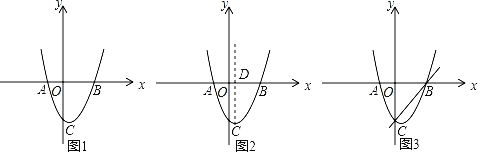
��1����Ò����ߵĽ���ʽ�ͶԳ��
��2����ͼ2�������ߵĶԳ�����x�ύ�ڵ�D���ڶԳ�������һ����E��ʹ��OAC����ODE���ƣ�ֱ��д����E�����ꣻ
��3����ͼ3��ƽ����x���ֱ���������߽���P��x1��y1����Q��x2��y2�����㣬��ֱ��BC���ڵ�N��x3��y3������x1��x2��x3ʱ�����ͼ����x1+x2+x3��ȡֵ��Χ��
���𰸡���1��y��x2��2x��3��x��1����2����E��1����3����1��3����1��![]() ����1����
����1����![]() ������3��x1+x2+x3��5
������3��x1+x2+x3��5
��������
��1���ɴ���ϵ�����������ʽ���ɵöԳ��
��2��������������ۣ������������ε����ʿɵ���⣻
��3���ɶ��κ��������ʿɵ�x1+x2=2��������ɵ�x3��3��������⣮
��1����������y��x2+bx��3��b�dz�������x�ύ��A��B���㣬
��0��1��b��3
��b����2��
�������߽���ʽΪ��y��x2��2x��3��
��y��0ʱ��x1����1��x2��3��
��B��3��0��
��Գ���Ϊֱ��x��1��
��2����������y��x2��2x��3��y�ύ�ڵ�C��
���C��0����3�����ҵ�A����Ϊ����1��0����
��OA��1��OB��3��
�ߡ�OAC����ODE���ƣ��ҡ�AOC����ODE��90����
��![]() ��
��![]() ��
��
��DE��3��![]() ��
��
���E��1����3����1��3����1��![]() ����1����
����1����![]() ����
����
��3���ߵ�B��3��0������C��0����3��
��ֱ��BC�Ľ���ʽΪ��y��x��3��
��ƽ����x���ֱ���������߽���P��x1��y1����Q��x2��y2�����㣬
���P����Q���ڶԳ���Գƣ�
��x1+x2��2��
��x1��x2��x3��
��ֱ��PQ��AB���Ϸ���
��x3��3��
��x1+x2+x3��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��ֱ��DE��AB�ڵ�F����BC�ڵ� M��DE���ӳ�����AC���ӳ��߽��ڵ�N������AM��
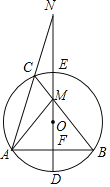
��1����֤��AM��BM��
��2����AM��BM��DE��8����N��15������BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������飬�ڵ�ʮ����ȫ���˴����ȫ���ȫ��������������������ע�ȷdz��ߣ���ҹ�ע�������ǹ�ע���ȵ㻰��ֱ��У����ѡ������������������������������࣬�ҹ�ע�����ȵ�����������������ռ�ٷֱ���ͼl��ʾ����ע�������ȵ���������������IJ���������ͳ����ͼ2��ʾ�������ͼ����Ϣ����������⣮

(1)���ͼl�й�ע���������������������ռ�ٷֱ�x��ֵ������ͼ2�еIJ�����������ͳ��ͼ����������
(2)Ϊ������̽�������������棬����������ɶ���5����������ס��ҡ������������������˷�̸����һ�η�̸ֻѡ2���������������б�������״ͼ�ķ��������һ����ѡ����ǡ���Ǽ��ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵���ÿ��50Ԫ�ļ۸�800��![]() ������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200�������̵�Ϊ���������������������ۣ������г����飬����ÿ����1Ԫ���ɶ����۳�10��������͵���Ӧ������50Ԫ���ڶ����½������̵��ʣ���T��һ������֣����ʱ����Ϊ40Ԫ����ڶ����µ��۽���
������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200�������̵�Ϊ���������������������ۣ������г����飬����ÿ����1Ԫ���ɶ����۳�10��������͵���Ӧ������50Ԫ���ڶ����½������̵��ʣ���T��һ������֣����ʱ����Ϊ40Ԫ����ڶ����µ��۽���![]() Ԫ��
Ԫ��
��1��������ú�![]() �Ĵ���ʽ��ɱ����еĢ٢ڢ۴���
�Ĵ���ʽ��ɱ����еĢ٢ڢ۴���
ʱ�� | ��һ���� | �ڶ����� | ��� |
���ۣ�Ԫ�� | 80 | _______ | 40 |
������������ | 200 | _______ | _______ |
��2��������̵�ϣ��ͨ��������800��![]() ������9000Ԫ����ô�ڶ����µ��۽��Ͷ���Ԫ��
������9000Ԫ����ô�ڶ����µ��۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD���߳�Ϊ4��E�DZ�BC�ϵ�һ���㣬��DE��ȡDE�е�G����GE��E˳ʱ����ת90����EF������CF����CEΪ_____ʱ��CFȡ����Сֵ��
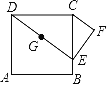
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() �ߵ��е㣬����
�ߵ��е㣬����![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
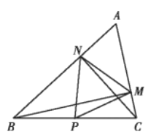
����![]() Ϊ�ȱ������Σ��ܵ�
Ϊ�ȱ������Σ��ܵ�![]() ʱ��
ʱ��![]() .�뽫��ȷ���۵�������ں�����__.
.�뽫��ȷ���۵�������ں�����__.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������IJ����У�װ�к졢�ơ�������ֻ����ɫ��ͬ��С�����к�ɫС����6�����ơ���ɫС���������ͬ��Ϊ���ƴ��л�ɫС���������ÿ�ν�����С����Ⱥ�����һ��С�������ɫ�Żأ��ٽ��ȶ�����鷢��������ɫ��Ƶ����![]() ������ƻ�ɫС��ĸ����ǣ�������
������ƻ�ɫС��ĸ����ǣ�������
A.21B.40C.42D.48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
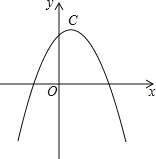
����Ŀ����ͼ��������C1��y1=��2x2+4x+2��C2��y2=��x2+mx+n�Ķ�����ͬ����
��1����������C2�Ľ���ʽ.
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
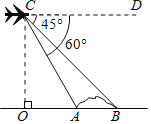
����Ŀ����ͼ��ij���ٹ�·��������Ҫȷ������AB�ij��ȣ���֪��C���ķɻ��ϣ�������Ա�����ǰ��A��B���㴦�ĸ��Ƿֱ�Ϊ60����45����AC�ij�Ϊ1000![]() m��������AB�ij���������������ţ�
m��������AB�ij���������������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com