
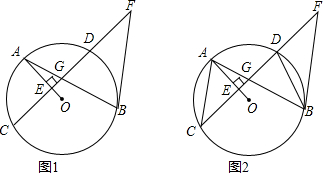
分析 (1)如图1,连接OB,根据等腰三角形的性质得到∠FBG=∠FGB,∠OAB=∠OBA,等量代换得到∠AGE=∠FBG,根据垂直的定义得到OB⊥BF,于是得到结论;
(2)由已知条件易证∠DGB=∠GDB,因为∠CAB和∠BDC都是弧BC所对的圆周角,所以∠CAB=∠BDC,进而可证明∠CAB=∠GBF,则AC∥BF;
(3)由(2)得∠FBG=∠CAG,再根据已知条件易证∠ACE=∠F,所以tan∠F=tan∠ACE=$\frac{3}{4}$,易求AE的长度.设⊙O的半径为R,根据勾股定理列方程求出R的值,然后又相似三角形的性质得到BF的长.
解答 证明:(1)如图1,连接OB,
∵BF=GF,
∴∠FBG=∠FGB,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠AGE=∠FGB,
∴∠AGE=∠FBG,
∵OA⊥CD,
∴∠AEG=90°,
∴∠AGE+∠EAG=90°,
∴∠OBG+∠FBG=90,
∴OB⊥BF,
∴BF是⊙O的切线;
(2)∵BD=BG,
∴∠DGB=∠GDB,
∵∠CAB和∠BDC都是弧BC所对的圆周角,
∴∠CAB=∠BDC,
∴∠CAB=∠FGB,
∵∠FGB=∠FBG,
∴∠CAB=∠GBF,
∴AC∥FB;
(3)由(2)得∠FBG=∠CAG,
∵∠FGB=∠FBG,
∴∠CAG=∠FGB,
∵∠FGB=∠CGA,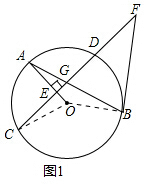
∴∠CGA=∠CAG,
∴CA=CG,
∵AC∥BF,
∴∠ACE=∠F,
∴tan∠ACE=tan∠F,
∵tan∠F=$\frac{3}{4}$,
∴tan∠ACE=$\frac{3}{4}$,
∴$\frac{AE}{CE}$=$\frac{3}{4}$,设AE=3k,CE=4k,
∴A=CG=5k,
∵AE⊥CD,
∴CE=DE=4k,
∴EG=k,DG=3k=3,
∴k=1,
∴AE=3,CE=4,
如图2,连接OC,设⊙O的半径为R,在Rt△CEO中,
CO2=CE2+OE2,即R2=42+(R-3)2,
解得R=$\frac{25}{6}$,
即⊙O的半径为$\frac{25}{6}$,
∵AG=$\sqrt{A{E}^{2}+E{G}^{\;}}$=$\sqrt{10}$,
∵AB,CD相交于G,
∴AG•BG=CG•DG,
∴BG=$\frac{3\sqrt{10}}{2}$,
∵BD=BG,BF=GF,
∴△BGD∽△FBG,
∴$\frac{BG}{BF}=\frac{DG}{BG}$,
∴BF=$\frac{B{G}^{2}}{DG}$=$\frac{15}{2}$.
点评 本题考查的是圆的综合题,涉及到切线的判定,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,相似三角形的判定和性质,熟练掌握和各种几何图形有关的定理及性质是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
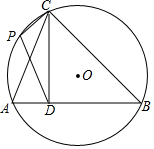 △ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.
△ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
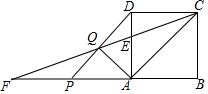 如图,在正方形ABCD中,AB=3,点E在AD边上,且DE=$\frac{1}{3}$AD,连结CE并延长交BA的延长线于点F,P是线段AF上一点(点P与点A、F不重合),连结PD,交CF于点Q,设AP=x,CQ=y.
如图,在正方形ABCD中,AB=3,点E在AD边上,且DE=$\frac{1}{3}$AD,连结CE并延长交BA的延长线于点F,P是线段AF上一点(点P与点A、F不重合),连结PD,交CF于点Q,设AP=x,CQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
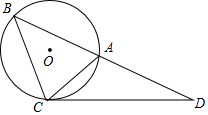 如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.
如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com