
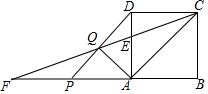
 如图,在正方形ABCD中,AB=3,点E在AD边上,且DE=$\frac{1}{3}$AD,连结CE并延长交BA的延长线于点F,P是线段AF上一点(点P与点A、F不重合),连结PD,交CF于点Q,设AP=x,CQ=y.
如图,在正方形ABCD中,AB=3,点E在AD边上,且DE=$\frac{1}{3}$AD,连结CE并延长交BA的延长线于点F,P是线段AF上一点(点P与点A、F不重合),连结PD,交CF于点Q,设AP=x,CQ=y.分析 (1)由正方形的性质得出AD=BC=CD=AB=3,∠ABC=∠ADC=∠BAD=90°,AB∥CD,由已知得出DE=1,AE=2,由平行线得出△CDE∽△FAE,得出对应边成比例,即可得出结果;
(2)由勾股定理求出CE=$\sqrt{10}$,得出FE=2CE=2$\sqrt{10}$,由平行线证出△FPQ∽△CDQ,得出比例式$\frac{PF}{CD}=\frac{FQ}{CQ}$,求出QE=$\frac{\sqrt{10}x}{9-x}$,即可得出y=$\frac{\sqrt{10}x}{9-x}$+$\sqrt{10}$,0<x<6;
(3)分两种情况:①∠AQC=90°时,证明△AQE∽△CDE,得出对应边成比例求出QE,即可得出x的值;
②∠CAQ=90°时,CQ为斜边;由正方形的性质得出∠DAC=45°,AC=3$\sqrt{2}$,证出AD平分∠CAQ,由角平分线定理得出$\frac{AQ}{AC}=\frac{QE}{CE}$,即$\frac{AQ}{3\sqrt{2}}=\frac{\frac{\sqrt{10x}}{9-x}}{\sqrt{10}}$,求出AQ=$\frac{3\sqrt{2}x}{9-x}$,在Rt△ACQ中,由勾股定理得出方程,解方程即可.
解答 解:(1)∵四边形ABCD是正方形,
∴AD=BC=CD=AB=3,∠ABC=∠ADC=∠BAD=90°,AB∥CD,
∵DE=$\frac{1}{3}$AD,
∴DE=1,AE=2,
∵BF∥CD,
∴△CDE∽△FAE,
∴$\frac{CD}{AF}=\frac{DE}{AE}$=$\frac{CE}{FE}$=$\frac{1}{2}$,
∴AF=2CD=6;
(2)∵∠ADC=90°,CD=3,DE=1,
∴CE=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴FE=2CE=2$\sqrt{10}$,
∵BF∥CD,
∴△FPQ∽△CDQ,
∴$\frac{PF}{CD}=\frac{FQ}{CQ}$,即$\frac{6-x}{3}=\frac{2\sqrt{10}-QE}{\sqrt{10}+QE}$,
解得:QE=$\frac{\sqrt{10}x}{9-x}$,
∴y=$\frac{\sqrt{10}x}{9-x}$+$\sqrt{10}$,
∵点P与点A、F不重合,
∴0<x<6;
(3)分两种情况:
①当∠AQC=90°时,
∴∠AQC═∠ADC,
∵∠AEQ=∠CED,
∴△AQE∽△CDE,
∴$\frac{QE}{DE}=\frac{AE}{CE}$,即$\frac{QE}{1}=\frac{2}{\sqrt{10}}$,
解得:QE=$\frac{\sqrt{10}}{5}$,
∴$\frac{\sqrt{10}x}{9-x}$=$\frac{\sqrt{10}}{5}$,
解得:x=$\frac{3}{2}$;
②当∠CAQ=90°时,CQ为斜边;
∵四边形ABCD是正方形,
∴∠DAC=45°,AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴∠DAQ=45°=∠DAC,
∴AD平分∠CAQ,
∴$\frac{AQ}{AC}=\frac{QE}{CE}$,即$\frac{AQ}{3\sqrt{2}}=\frac{\frac{\sqrt{10x}}{9-x}}{\sqrt{10}}$,
解得:AQ=$\frac{3\sqrt{2}x}{9-x}$,
在Rt△ACQ中,由勾股定理得:AQ2+AC2=CQ2,
即($\frac{3\sqrt{2}x}{9-x}$)2+(3$\sqrt{2}$)2=($\frac{\sqrt{10}x}{9-x}$+$\sqrt{10}$)2,
解得:x=2,或x=6(舍去),
∴x=2;
综上所述:当△ACQ是直角三角形时,x的值为$\frac{3}{2}$或2.
点评 本题是四边形综合题目,考查了正方形的性质、相似三角形的判定与性质、勾股定理、角平分线定理等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键,注意分类讨论.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
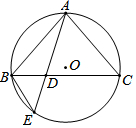 如图,△ABC内接于⊙O,且AB=AC,E是弧BC上一点,AE交BC于点D.
如图,△ABC内接于⊙O,且AB=AC,E是弧BC上一点,AE交BC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2! | B. | 2450 | C. | $\frac{25}{24}$ | D. | 49! |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x/万元 | 30 | 80 | 120 |
| y/万元 | 44 | n | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
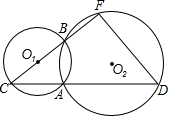 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com